Порог чувствительности измерительной системы. Чувствительность к форме сигнала. Пределы измерений, динамический диапазон, страница 9

Это частный случаи уравнения вида:

y=ax+b

Здесь b либо имеет нулевое значение, либо играет роль начального смещения, а а — чувствительность. Время установления t_s равно нулю, а ширина полосы f0 равна бесконечности. В действительности, конечно, на очень высоких частотах чувствительность уменьшается, и у этого много причин (упругость, масса, паразитная емкость и т. д ); поэтому часто говорят, что такие системы являются системами квази-нулевого порядка. Это означает, что реакция таких систем является мгновенной в том диапазоне частот, который существенен при измерении данной величины. Систему, изображенную на рис. 2.38(b), также можно считать системой нулевого порядка. Выходное напряжение датчика Холла V_H пропорционально току I_H, протекающему по пластине Холла и индукции В магнитного поля, образуемого центральным проводником.

Кроме того, будет иметь место начальное смещение V₀. В разделе 3.2.3 будет показано, что

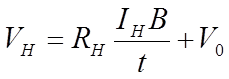
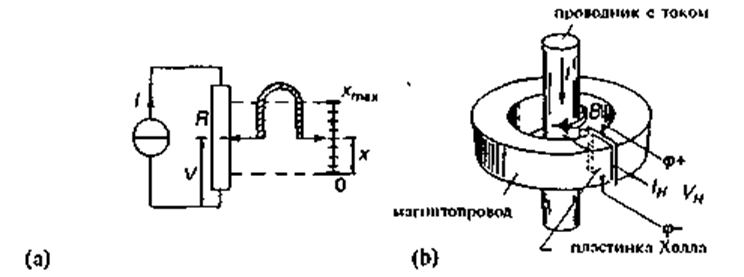
Рис 2 38 Системы нулевого порядка (а) потенциометрический преобразователь смещения и (b) датчик тока.

Здесь R_H — постоянная Холла для данной пластины, а t — ее толщина Поскольку значение В пропорционально току, текущему по центральному проводнику, такой датчик исключительно удобен для измерения больших токов. Он позволяет осуществить такое измерение, не разрывая проводник для подключения пробника, который внес бы дополнительное сопротивление.

Системы первого порядка

У линейных систем первого порядка соотношение между входным сигналом х(t) и выходным сигналом y(t) выражается линейным дифференциальным уравнением первого порядка. Простой пример такой системы — ртутный термометр. Изменение длины столбика ртути, определяемое по откалиброванной шкале, служит выходным сигналом, а входным сигналом является измеряемая температура окружающей среды Тi. Мы будем предполагать, что изменение длины столбика ртути прямо пропорционально изменению температуры ртути в резервуаре термометра. Поэтому для описания динамического поведения термометра вполне можно принять температуру Т₀ ртути в резервуаре за выходную величину (см рис. 2.39(а)). Теплообмен между ртутью в резервуаре и окружающим воздухом должен происходить через стеклянную стенку с тепловым сопротивлением R. Тепловую емкость (теплоемкость) ртути в резервуаре обозначим С. Для малого приращения тепла ΔQ получим:

Кроме того,

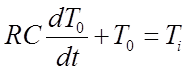
Поэтому

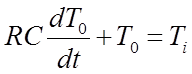
Другой пример системы первого порядка — это RС-цепь, приведенная на рис. 2.39(b). Пусть Vi и V₀ — входное и выходное напряжения. С учетом того, что

и

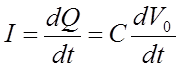
Рис. 2.39. Два примера систем первого порядка: (а) ртутный термометр и (b) RC – цепь.

Находим:

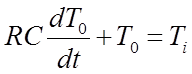
Полагая в обоих случаях RC = τ, мы можем представить эти линейные дифференциальные уравнения первого порядка в следующем общем виде:

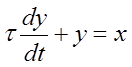
где х = х(t), а у = y(t) Таким образом, мы можем придти к выводу, что ртутный термометр и R С- цепь эквивалентны с точки зрения их динамического поведения. Это дифференциальное уравнение решается просто. При скачкообразном входном сигнале

   x(t)=x₀

 

при t > О

и x(t)=0 при t <0

а выходной сигнал   у(t), или переходную характеристику, находим из

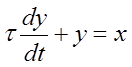
В операторной форме уравнение имеет вид:

Откуда

Общее решение таково:    у = С.

Частным решением при t → ∞  является функция y(t) = у₀ (конечное или установившееся значение):

Полагая, что   у(t)= 0 при   t = 0, найдем:

Таким образом, переходная характеристика измерительной системы первого порядка имеет вид где у₀ - конечное или установившееся значение, а τ = RC- постоянная времени. Эта переходная характеристика изображена на рис.2.40.

Если относительная погрешность измерительной системы не может превосходить e= Δy_о /y_о, то время установления t_s равно

t_s = -τ lпе