Порог чувствительности измерительной системы. Чувствительность к форме сигнала. Пределы измерений, динамический диапазон, страница 5

Разрешающая способность

Разрешающая способность (разрешение) измерительной системы — это размер шага, на который может быть настроена система, или шага, с которым на индикатор выводится результат действия системы. По определению, разрешающая способность — это наименьший интервал Dх значения измеряемой величины х, который все еще вызывает изменение результата измерения у. Численно разрешающая способность R выражается в виде:

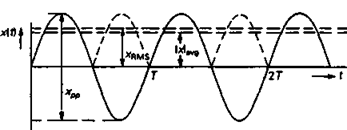
Рис. 2.30. Полный размах х_pp, действующее значение х_rms, и среднее значение от абсолютной величины |x|avg сигнала синусоидальной формы.

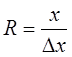
Иногда речь идет о максимальном значении разрешения. Оно достигается при максимальной величине х, которая может быть измерена с помощью этой системы без насыщения, искажений и перегрузки:

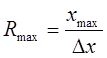
Разрешающая способность R имеет конечное значение для всех систем, в которых результат измерения не увеличивается непрерывно с ростом измеряемой величины х. Примером таких систем являются механическая измерительная система с люфтом и трением покоя, проволочный потенциометр, ступенчатый аттенюатор и цифровой индикатор; во всех этих случаях выходная величина у не растет непрерывно с увеличением входного воздействия, а меняется малыми скачками Dу.

Если разрешение системы конечно, то результат измерений оказывается квантованным; при этом возникает ошибка квантования. Ошибки, являющиеся следствием квантованности результата измерения, можно разделить на ошибки усечения и ошибки округления Ошибка усечения происходит в том случае, когда в системе не принимаются во внимание десятичные знаки справа от младшего указываемого десятичного разряда: остаток просто опускают. Обычно это имеет место в алфавитно-цифровых индикаторах, например, в цифровом вольтметре. Величина допускаемой при этом ошибки равна Dх / х, то есть отношению наименьшего возможного шага Dх к воспроизводимой на индикаторе величине х. Ошибка округления происходит в том случае, когда в наименьшем указываемом десятичном разряде учитывается остаток путем округления до ближайшего значения в этом разряде При этом ошибка равна Dх /2х, то есть половине наименьшего шага, деленной на индицируемое значение. Если при проведении нуль-измерения мы применим эталон, который можно подстраивать только в ступенчатом режиме, и будем изменять задаваемую эталоном величину до тех пор, пока нуль-орган не покажет наименьший отсчёт, то будет иметь место ошибка округления.

Нелинейность

В измерительной системе с независящей от частоты чувствительностью соотношение между выходным сигналом у и входным сигналом х линейно, когда функция у =f(x) представляет собой прямую линию; такие системы с частотно-независимой чувствительностью, у которых f(x) = ах + b, называют статическими системами. Для линейной частотно-зависимой системы соотношение между y(t) и x(t) задается линейным дифференциальным уравнением Это такое уравнение, в котором содержатся только члены первого порядка в отношении у и производных от у. Системы с частотно-зависимой чувствительностью называют динамическими системами. Если на вход линейной измерительной системы подать сумму двух синусоидальных сигналов х₁ = а₁ sin(w₁t + ф₁) и х₂ = а₂ sin(w₂t + ф₂), то выходной сигнал также будет состоять из двух синусоидальных сигналов у₁ = b₁sin(w₁t + ф_о1) и y₂=b₂sin(w₂t +ф_о2) с теми же самыми частотами, что и во входном сигнале (изохронизм), но уже с другими амплитудами и фазами.

Для линейных систем справедлив принцип суперпозиции; это означает, что в случае, когда входной сигнал x_l порождает на выходе сигнал у₁, а входной сигнал х₂ вызывает появление на выходе сигнала у_г линейная комбинация ах₁ + Ьх₂ на входе приведет к возникновению на выходе сигнала ау₂ + bу_г. Принцип суперпозиции применим только к тем составляющим сигнала на входе системы, которые обусловлены входными воздействиями; возможные ошибки смещения здесь не принимаются во внимание.