Порог чувствительности можно также улучшить, сужая ширину полосы В измерительной системы. В предположении, что шум белый, находим его среднеквадратическое значение σ.
![]()
где а0- эквивалентный шум в полосе 1 Гц. Это означает, что с сокращением полосы В измерительной системы в какое-то число раз, во столько же раз увеличивается отношение сигнал/шум. Соответственно этому снижается порог чувствительности.
В качестве альтернативы нахождению среднего от п отдельных последовательных выборок мы можем также измерять входной сигнал x(f) непрерывно в течение определенного времени Т.
Среднее по времени значение уavg выходного сигнала измерительной системы y(t) на интервале (t, t + Т) равно:
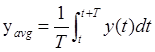
Теперь можно воспользоваться этим средним, чтобы установить, имеется сигнал на входе или его нет. Чтобы определить результирующее улучшение порога чувствительности, применим теорему Шеннона о выборках, которая звучит так: если у сигнала y(f) нет составляющих на частотах выше, чем В Гц, то этот сигнал полностью определяется выборками, взятыми с интервалом 1 / 2В секунд на отрезке времени Т, много большем чем 1 / В. Число дискретных выборок, описывающих y(t) на отрезке Т секунд, равно 2ТВ. Возьмем среднее от этих 2ТВ выборок. Среднеквадратическое значение шума в сигнале y(t) равно σ = σ 0√B. Таким образом, стандартное отклонение σavgсреднего по выборкам из сигнала y(t) на протяжении Т секунд имеет вид:
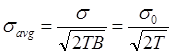
Следовательно, вычисление среднего на интервале времени Т приводит к увеличению отношения сигнал/шум в 2T раз; порог чувствительности снижается в √2Т раз
Подводя итоги, мы можем утверждать, что порог чувствительности — это наименьший сигнал, который можно обнаружить с определенной степенью достоверности на фоне собственного шума измерительной системы. Порог чувствительности зависит от требуемой достоверности и величины шума в измерительной системе. Шум можно уменьшить, применяя измерительную систему с меньшей шириной полосы или вычисляя среднее для ряда выборочных значений, полученных в результате измерений, а также путем нахождения среднего по времени при непрерывном измерении на интервале времени Т. Все эти меры требуют затраты большого времени для получения результата; как следствие их применения, отклик измерительной системы становится более медленным, и это является платой за снижение собственного порога чувствительности измерительной системы.
Чувствительность к форме сигнала
Сигнал на входе измерительной системы служит носителем информации о значении физической величины, которая должна быть измерена. Отклик системы на входной сигнал в общем случае зависит от формы (вида или структуры) этого входного сигнала.
Часто классификацию сигналов проводят по следующим признакам. Сигнал может быть константой, то есть не зависеть от времени (статический сигнал), например, постоянное напряжение или постоянный ток. Обычно сигнал изменяется, но только очень медленно; такой сигнал называют квазистатическим. Однако не менее часто сигнал является функцией времени (динамический сигнал). Если сигнал x(t) повторяется во времени каждые Т секунд, то он называется периодическим сигналом с периодом T (для всех t x(t) = x(t +T); см. рис. 2.29(а)). Частота повторения равна f = 1 / Т. Отношение Δt/T для импульсных сигналов (см. рис. 2.29(b)), по определению, представляет собой коэффициент заполнения. Сигналы с очень малым коэффициентом заполнения (импульсы) измерять трудно, и часто они являются причиной сильных наводок на соседние измерительные устройства. Когда зависящий от времени сигнал не является периодическим, его называют одиночным сигналом (одиночной реализацией) или неустановившимся сигналом (переходным процессом). Примерами таких сигналов служат шумовые напряжения и переходные явления, такие как выбросы или звон (затухающие колебания) в системах с переключениями. Как правило, периодические сигналы легче измерять, чем непериодические. В частности, поэтому при исследовании переходной характеристики системы условия ее воспроизведения повторяют многократно, получая, таким образом, более легкий для измерения периодический сигнал.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.