Порог чувствительности измерительной системы. Чувствительность к форме сигнала. Пределы измерений, динамический диапазон, страница 14

Рис 2 47. Зависимость амплитуды основной гармоники вынужденных колебаний нелинейной системы «пружина с грузом» от частоты синусоидального воздействия постоянной амплитуды при наличии демпфирования (в случае, когда жесткость пружины увеличивается).

характерен для линейной системы второго порядка и показан на рис. 2.45(а). Она теперь наклонена в сторону более высоких частот; другими словами, она теперь перекошена. Если амплитуда F_d синусоидального воздействия меняется, то пик резонансной кривой будет перемещаться по штриховой линии, которая является характеристикой свободных колебаний (как на рис. 2.46(b), β > 0).

Если частота возбуждающей силы увеличивается, но амплитуда F_dостается постоянной, то выходная величина в системе «пружина с грузом» внезапно падает до много меньшего уровня (явление перескока) после того, как на частоте w = bw₀ достигается пик резонансной кривой. Когда частота уменьшается (опять же при неизменной амплитуде входного воздействия), амплитуда основной гармоники в сигнале l(t) вдруг скачком переходит к большему значению на частоте w = aw_0.Следовательно, в интервале частот     bw₀ ≤w≤ bw₀система неустойчива. Установившийся режим никогда не может принадлежать кривой, изображенной точками внутри этого интервала. Мы видим, что резонансные кривые такого рода нелинейных механических систем обладают гистерезисом.

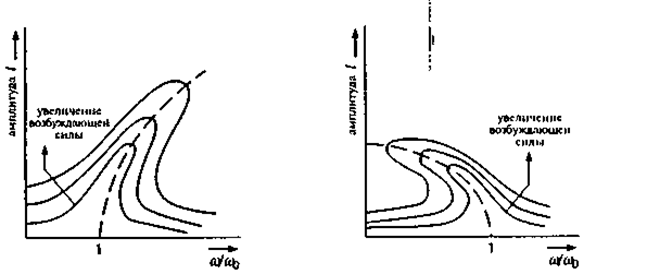
Если мы теперь вдобавок станем изменять амплитуду возбуждающей силы f_d(t), то получим резонансные кривые, представленные на рис. 2.48. На рис. 2.48(а) показаны характеристики системы «пружина с грузом» в случае, когда жесткость пружины постепенно увеличивается, а на рис. 2.48(b) — для случая, когда жесткость пружины уменьшается.

(a)  (b)

Рис. 2 48 Влияние амплитуды входного воздействия на резонансные кривые (см рис 2 47) нелинейной системы «пружина с грузом» при наличии демпфирования. На рис. (а) представлен случай, когда жесткость пружины увеличивается (b > 0), а на рис. (b) показаны амплитудно-частотные характеристики для случая, когда пружина постепенно становится мягче (b < 0).

Наконец, обратим внимание на тот факт, что у систем такого рода при возбуждении их синусоидальным воздействием, помимо высших гармоник на частотах kw, могут наблюдаться субгармоники на частотах w / п (здесь k и п — целые числа). Обычно это происходит при малом, но не равном нулю затухании D_t.

Приведенный иллюстративный пример поведения нелинейной динамической системы ясно показывает, насколько сложными могут быть эти системы. Это обстоятельство является одной из причин, по которым в измерительных системах стараются избежать сколько-нибудь существенной (динамической) нелинейности: система становится слишком сложной.

2.3.3.3 Помехи

В разделе 2.3.3 мы видели, что взаимодействие между измерительной системой и измеряемым объектом состоит не только из желаемого воздействия объекта на измерительную систему, но и включает в себя также нежелательную реакцию объекта на подключение к измерительной системе. Как было показано, эту реакцию можно значительно ослабить, осуществляя сопряжение измерительной системы с измеряемым объектом.

В этом разделе мы рассмотрим взаимодействие между измерительной системой и ее окружением (см. рис. 2.49). Влияние окружающей среды на измерительную систему может сказаться на результате измерения, и потому оно является нежелательным и вносящим помехи.

Такое мешающее окружение может влиять на измерительную систему двумя способами: аддитивно и мультипликативно. В случае аддитивных помех параметр d, выражающий мешающее воздействие окружающей среды, вызовет появление сигнала у на выходе измерительной системы даже тогда, когда входной сигнал х отсутствует (измеряемая величина не подана на вход). Этот выходной сигнал складывается с той частью выходного сигнала, которая возникает при подаче на вход измеряемого сигнала х. Система откликается таким образом, как если бы у нее была такая передаточная функция, благодаря которой помеха могла бы «просачиваться» на выход у. Поэтому мерой того, в какой степени выходной сигнал подвержен влиянию помехи d, служит соответствующая чувствительность, а именно чувствительность по отношению к помехе (или коэффициент чувствительности) S_d: