Порог чувствительности измерительной системы. Чувствительность к форме сигнала. Пределы измерений, динамический диапазон, страница 16

S₂ C_d1= - S_d2

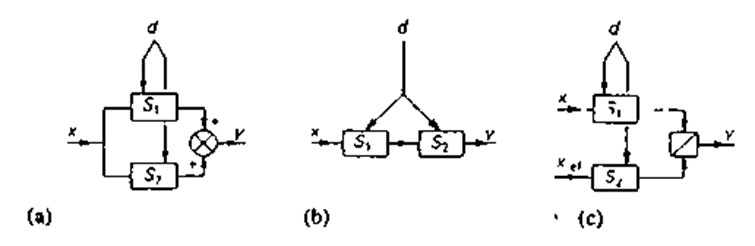
Рис 2 50 Три основных метода компенсации помex, возникающих в результате влияния окружающей среды (а) параллельная компенсация, (b) последовательная компенсация и (с) компенсация путём вычисления отношения.

то аддитивные помехи уже не оказывают своего влияния, а действие мультипликативной помехи полностью подавляется, когда

C_d1 = -  C_d2

Следует отметить, что последнее утверждение справедливо только в том случае, когда относительные изменения чувствительности подсистем S₁ и S₂ под влиянием помехи d (обозначаемые соответственно ΔS₁ /S₁ и  ΔS₂ /S₂) много меньше 1

Наконец, метод компенсации путем вычисления отношения эффективен только при борьбе с мультипликативными помехами.Чувствительность системы, в которой берется отношение, равна S = S_{/S₂x_ref , где x_ref — постоянная опорная величина. Внешняя мультипликативная помеха воздействует как на S₁, так и на S₂ Эта мультипликативная помеха подавляется в выходном сигнале, если

C_d1 =  C_d2

Примером параллельной компенсации является дифференциальный усилитель с резистором в общей цепи эмиттеров. Ошибка смещения нуля двух входных биполярных транзисторов, равного 650 мВ, с температурным коэффициентом 2,5 мВ/К, уменьшается здесь до значения, приблизительно равного 1 мВ, с температурным коэффициентом      ±2 мкВ/К. Последовательная компенсация часто применяется для борьбы с помехами в измерительных преобразователях. Помеха компенсируется в схеме, включенной последовательно с источником измеряемого сигнала. Наконец, компенсация путем вычисления отношения происходит де-факто при любом измерении отношения.

— Можно изменить форму входного сигнала или его частотный спектр так, чтобы помеху можно было легко отделить от полезного сигнала. Например, в усилителе постоянного тока с преобразованием от постоянного напряжения, поступающего на вход, переходят к переменному сигналу (см раздел 3.3.4). Это позволяет избежать влияния смещения по постоянному току и дрейфа внутри самого усилителя.

—  Для борьбы с мультипликативными помехами можно воспользоваться обратной связью.На рис. 2.51. представлена схема, в которой за счет обрат ной связи из сигнала х на входе измерительной системы с чувствительностью S₀ вычитается β-ая часть выходного сигнала у.Чувствительность S_f системы в целом, с учетом обратной связи, уже не равна S_0, а определяется соотношением

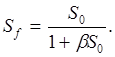
Предположим, что   S₀ зависит от температуры и температурный коэффициент равен

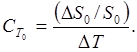
Температурный коэффициент С_Tf  системы с обратной связью тогда равен

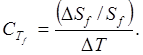
Поскольку

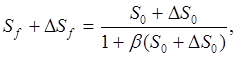
отсюда следует, что

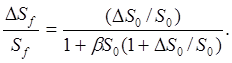
При малых отклонениях ΔS₀/S₀ << 1; поэтому

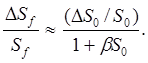
и, следовательно

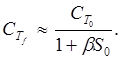
Говорят, что при |l + βS₀| > 1 обратная связь отрицательна, а при|l + βS₀| < 1 обратная связь положительна. Когда отрицательная обратная связь является глубокой, коэффициент помехи значительно уменьшается. Однако в этом случае и чувствительность, равная S_f ≈ 1 / β оказывается много меньшей, чем чувствительность S₀ исходной системы. Поэтому для достижения определенного значения чувствительности S_f которая была бы свободна от влияния помех, необходимо, чтобы значение коэффициента передачи β было, по возможности, более точным и не зависело бы от действия помех Теперь чувствительность системы определяется величиной βЗа ослабление действия

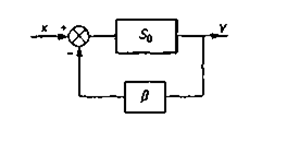
Рис. 2.51. Применение обратной связи в измерительной системе с исходной чувствительностью S_0.

помех мы платим уменьшением чувствительности системы от исходного значения   S₀ до величины 1 / β.

Отметим, что за счет отрицательной обратной связи аддитивные помехи уменьшаются во столько же раз, во сколько уменьшается чувствительность системы. Это означает, что отношение измеряемого сигнала к помехе (как на входе, так и на выходе) не меняется в результате введения обратной связи. Точно так же, в результате применения отрицательной связи отношение сигнал/шум измерительной системы не улучшается. Мы еще вернемся к вопросу об отрицательной обратной связи в разделе 3.3.4.

Сейчас мы рассмотрим несколько часто встречающихся источников по мех, ограничившись только такими из них, с которыми приходится иметь дело в электронных измерительных системах.