Порог чувствительности измерительной системы. Чувствительность к форме сигнала. Пределы измерений, динамический диапазон, страница 12

Обычно измерители с подвижной катушкой бывают сконструированы таким образом, чтобы демпфирование у них было кг точно критическим, а слегка недостаточным (z = 1/) Из-за этого происходит небольшое проскакивание стрелки (4%) Достоинство такого подхода состоит в том, что наблюдатель яснее видит, когда стрелка устанавливается на конечном значении. У такого значения коэффициента затухания z применительно к измерительным системам есть и другое достоинство: при z » 0,7 амплитудно-частотная характеристика оказывается горизонтальной в возможно более широком диапазоне частот (этот вопрос рассмотрен ниже; см рис 2.45).

Избыточное демпфирование (z > 1)

При тех же начальных условиях, что и выше, но с коэффициентом затухания z больше единицы, переходная характеристика y(t) как реакция на входной скачок величины х₀ в момент t = 0 имеет вид:

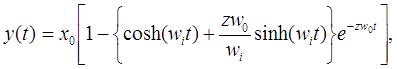
где . В данном случае выходная величина будет постепенно приближаться («ползти») к конечному значению у₀ = х₀ (см. рис 2 43)

Постоянная времени прибора или его время установления (готовности) t_s зависит от коэффициента затухания z, периода T₀, соответствующего частоте свободных колебаний (T₀ = 2p/w₀), и, естественно, от допустимой относительной ошибки в конечной величине Dу₀/у₀ (см. рис. 2.44) У кривых на этом графике имеются разрывы при z < 1, обусловленные тем, что при заданных значениях T₀ и относительной погрешности (скажем 0,1%) время готовности t_s увеличивается скачками при непрерывном уменьшении коэффициента затухания z. Причина скачков заключается в том, что время готовности каждый раз увеличивается на один период затухающих колебаний

Частотную характеристику системы второго порядка легко найти, рассматривая RLC -аналог такой системы, показанный; на рис 2 42(с):

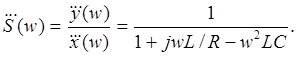
Амплитудно-частотная характеристика имеет вид:

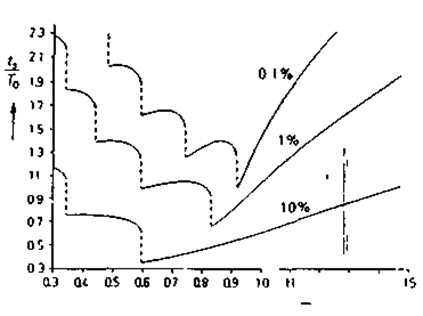
Рис. 2. 44. Время установления (готовности) t_s системы второго порядка при различных значениях допустимой относительной ошибки Dу₀ / у₀в конечном результате у_а Т_а — период свободных колебаний, а z — относительный коэффициент затухания системы.

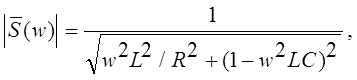
а для фазовой характеристики справедливо соотношение:

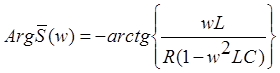
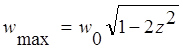Подставляя z² = L/4R²C и w= 1/LC , можно написать эти выражения в общей форме. Дифференцируя  по w,находим, что максимум  достигается при  и значение  в максимуме равно

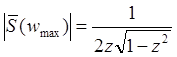
(при z≤)

Частотная характеристика оказывается плоской в возможно более широком диапазоне частот, если , то есть в случае, когда z =. При этом ширина полосы системы равна f₀ = w₀/2π, где tw₀ — частота свободных колебаний. В точке w = w₀фазовый сдвиг равен —90°. На очень высоких частотах сдвиг по фазе стремится к —180°, но никогда не превышает этого значения, а величина сигнала на выходе системы при этом почти равна нулю Если z < , то амплитудно-частотная характеристика имеет пик на частоте затухающих колебании (см рис.2 45 (а) и (b)).

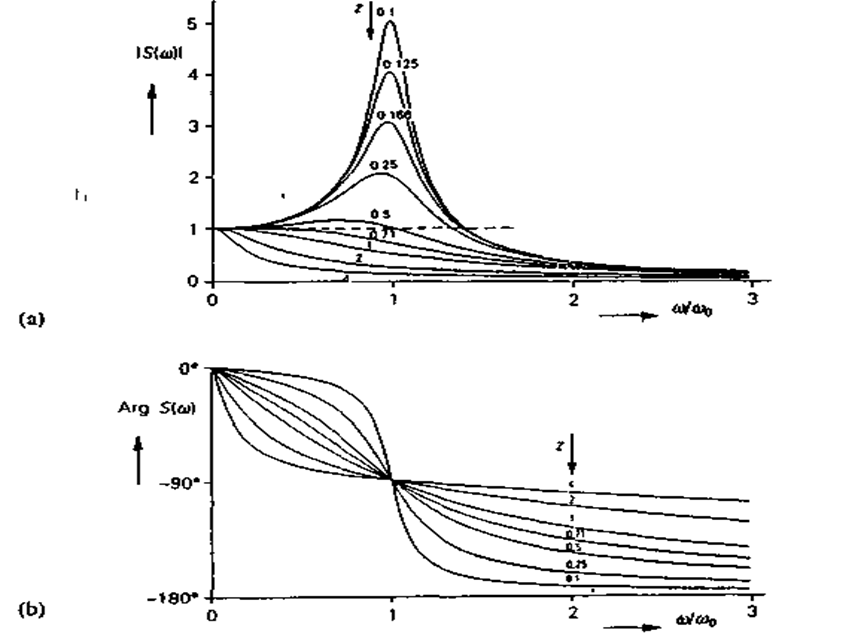
Рис. 2.45. (а) Амплитудно-частотная и (b) фазо-частотная характеристики системы второго порядка при различных значениях коэффициента затухания z.

Нелинейные системы

До сих пор мы рассматривали отклик систем, предполагая, что они являются линейными. Но что произойдет, если эти системы нелинейны?На рис. 2.32 уже было показано, что по мере того, как входные величины становятся достаточно большими, всякая реальная система, в конце концов, становится нелинейной из-за насыщения, перегрузки или ограничения. Сейчас на простом механическом примере мы проиллюстрируем, что происходит при этом с откликом.

Рассмотрим классический метод определения механической силы с помощью пружинного измерителя, в котором сила F_d приложенная к внутренней пружине, преобразуется в пропорциональное изменение l длины пружины. Пусть штифт или кольцо, с помощью которых усилие передается пружине, обладают определенной массой, а о пружине предполагается, что у нее есть некоторое затухание Тогда при малом входном воздействии, когда сила мала, и малом соответствующем изменении длины, можно воспользоваться аналогом, изображенным на рис. 2.42(b). Когда l мало, статическое поведение пружинного измерителя силы определяется законом Гука: F_d = K_tl,