Это легко получить из выражения для переходной характеристики с помощью графика на рис. 2.40. Когда требуется очень малая относительная ошибка Δyо /yо в конечном отсчете на выходе такой системы первого порядка, ее время установления ts становится чрезмерно большим. В примере с термометром на рис. 2.39(а) столбик ртути все медленнее ползет вверх к конечной отметке, которая достигается только при наступлении теплового равновесия между системой и ее окружением. Это является нежелательным свойством отклика первого порядка, когда речь идет о точных измерениях; время установления будет слишком большим.
Частотная характеристика — это, по существу, отклик системы на синусоидальный входной сигнал x(t)= xsin(wt) в установившемся режиме, то есть отклик, спустя длительное время после включения сигнала и подачи его на вход, когда все переходные явления затухнут. Частотную характеристику находят как частное решение дифференциального уравнения, описывающего систему первого порядка, при t → ∞ .
Частотную характеристику легко получить, применяя комплексные переменные в электрическом аналоге системы первого порядка, приведенном на рис.2.39.(b). Это даёт:
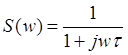 |
(при t = RC )
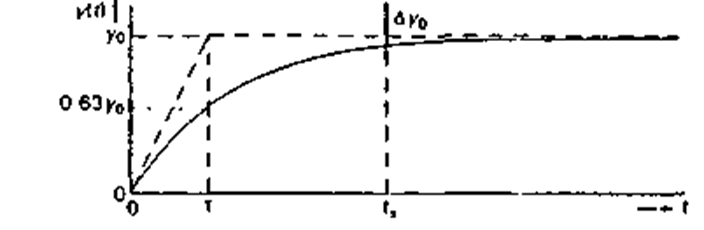
Рис 2 40. Переходная характеристика системы первого порядка.
Модуль S(w) равен
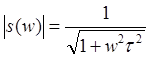
a аргумент S(w)имеет вид:
Arg S(w) = -arctg wt .
Амплитудно-частотная характеристика S(w) и фазо-частотная характеристика Arg S(w) системы первого порядка представлены на рис 241. Ширина полосы f0 системы первого порядка определяется из равенстпа wt = 1, так что f0 = 1 / 2πt. На этой частоте сдвиг по фазе уже достигает значения -.π/4 или -45˚. На более высоких частотах сдвиг по фазе стремится к -90°, тогда как амплитуда выходного сигнала уменьшается почти до нуля.
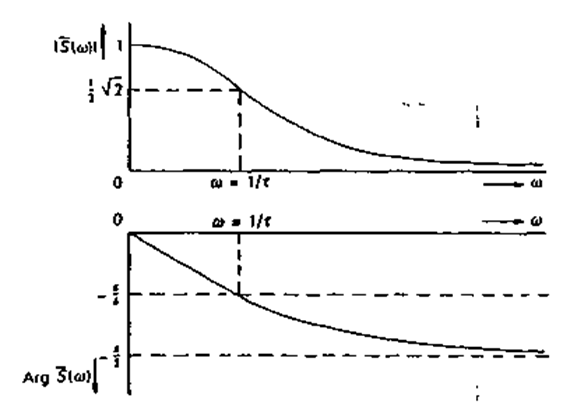
Рис. 2.41. Частотная характеристика системы первого порядка.
Системы второго порядка
В качестве примера системы второго порядка мы воспользуемся конструкцией стрелочного прибора (в частности, измерителя с подвижной катушкой), которая представляет собой вращающуюся механическую систему Каждая из следующих четырех механических пар сил оказывает воздействие на вращающуюся часть измерителя, создавая вращающий момент рис 2.42(а):
- Отклоняющее воздействие. Это воздействие вызывает отклонение стрел ки на угол θ. Момент этого воздействия пропорционален измеряемой вели чине (току). Мы обозначим этот момент Md
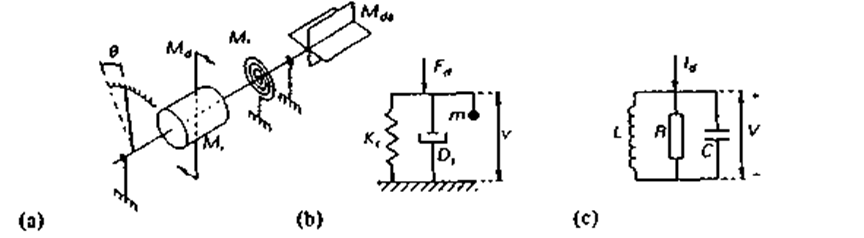
Рис 2 42 Системы второго порядка: (а) механическое вращение; (b) механическое поступательное движение; (с) параллельный электрический контур.
- Возвращающее воздействие. Это воздействие оказывает противодействие отклонению стрелки. В данном примере оно создается спиральной пружиной; вращающий момент этого воздействия обозначается Мr. Когда достигается установившееся состояние, отклоняющий момент и возвращающий момент равны: Мd = Мr Обычно бывает так, что возвращающий момент пропорционален углу отклонения θ, то есть Мr = Кr θ, где Кr — коэффициент упругости (жесткость пружины).
- Демпфирующее воздействие. Это воздействие также противодействует отклоняющему моменту. Демпфирующий момент пропорционален угловой скорости стрелки, так что Мda = Dr dθ / dt. Здесь Dr — постоянная затухания вращающейся конструкции. Затухание линейно зависит от угловой скорости dθ / dt.
Демпфирование применяют для того, чтобы предотвратить проскакивание стрелки за конечное значение и колебания стрелки вокруг него. Для этого используют те или иные крыльчатые приспособления и поршни (воздушное демпфирование), а также индукцию вихревых токов в металлической пластине в случае движущихся систем (демпфирование за счет токов Фуко).
Инерционность. Инерция вращающейся конструкции измерителя приводит к возникновению еще одного противодействующего момента, который пропорционален угловому ускорению стрелки, так что
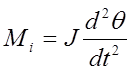
где J — момент инерции вращающейся конструкции относительно оси вращения.
Динамическое поведение измерителя определяется его уравнением движения; в любой момент времени отклоняющий момент уравновешивается суммой всех других моментов:
Мi + Mda + Mr = Md,
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.