Известно, что обратная связь уменьшает влияние изменений параметров устройств, образующих прямой канал системы, т.е. объекта управления, исполнительного механизма, преобразователя и т.д. Рассмотрим простую систему с единичной обратной связью (рисунок 3.1).
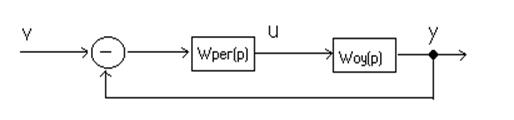
На рисунке 3.1 использованы обозначения Wоу (р), Wрег (р) – передаточные функции объекта управления и регулятора соответственно. Определим передаточную функцию замкнутой системы
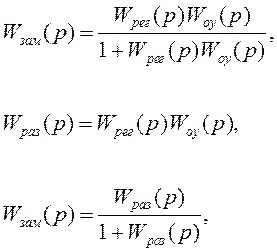
Чувствительность свойств замкнутой системы от свойств разомкнутой определяется выражением
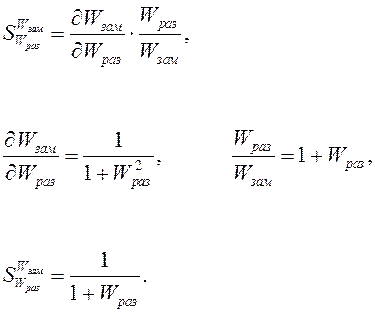
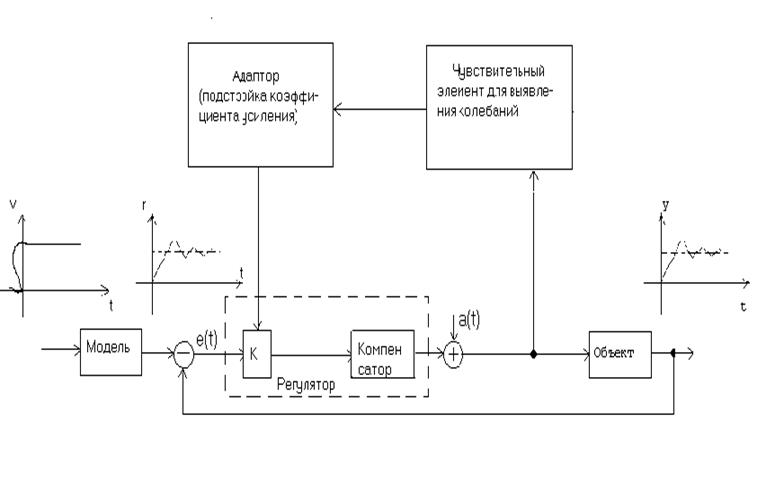
Таким образом, чувствительность обратно пропорциональна множителю (1+Wраз). Если величина Wраз (p) может быть достаточно большой, хотя бы за счёт увеличения коэффициента передачи регулятора, то чувствительность к изменению параметров Wраз(p) будет уменьшена. Однако увеличение коэффициента передачи ограничено условиями устойчивости и рабочими характеристиками. Эти ограничения можно преодолеть в ряде случаев, если ввести в систему цепь адаптации. Адаптивная система с большим коэффициентом усиления была представлена в виде автопилота корпорацией Миннеаполис – Ханивелл (Prince L.T., Hendrick R.C., Lindahl J.H. Honney well’s Flight Control System, Symposium on Adaptive Control, 1960) (рисунок 3.2).
 .
.
Коэффициент передачи и, как следствие, ширина зоны пропускания поддерживаются на самом высоком уровне с помощью цепи адаптации. При большом коэффициенте передачи замкнутая система приближается к границе устойчивости. Так как Wзам(р) » 1, выходная переменная системы достаточно близка к эталонному входному сигналу (r (t)). Эталонный входной сигнал можно получить с помощью простой модели (например, с помощью электрической цепи), и чтобы адаптация давала приемлемую точность, необходимо установить полосу пропускания модели на уровне 1/3 ширины пропускания замкнутой системы. При этих условиях адаптивная система практически нечувствительна к изменениям параметров объекта управления.)
Изменение коэффициента передачи зависит от колебательности процессов в системе. На наличие колебаний проверяется либо управляющий сигнал, либо сигнал ошибки.
К основным недостаткам системы относятся то, что
1) модель объекта управления должна быть известна для того, чтобы удерживать полюсы замкнутой системы достаточно далеко от мнимой оси;
2) в цепи управления постоянно присутствуют небольшие колебания. На практике амплитуда колебаний может поддерживаться на уровне ниже порога чувствительности пилота, и поэтому она может не влиять на полет.
3.2 Синтез адаптивных систем градиентным методом
Градиентный алгоритм относится к базовым алгоритмам
адаптации. Вектор градиента всегда направлен в сторону максимального локального
роста функции. Следовательно, если вектор скорости настраиваемых параметров (![]() ) направить в сторону антиградиента
) направить в сторону антиградиента 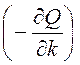 , то реализуется последовательный спуск в
локальный минимум
, то реализуется последовательный спуск в
локальный минимум
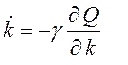 (3.1)
(3.1)
Общий подход к последовательности синтеза системы градиентным методом рассмотрим на примере скалярного объекта первого порядка:
![]() .
.
Эталонной модели можно поставить в соответствие уравнение вида
![]() ,
,
где
![]() . Обозначим рассогласование между
. Обозначим рассогласование между ![]() и
и ![]() через e
:
через e
: ![]() . Цель функционирования системы можно
задать асимптотическим выражением:
. Цель функционирования системы можно
задать асимптотическим выражением: ![]() при
при ![]() . Используя известные методы синтеза, закон
управления получим в виде:
. Используя известные методы синтеза, закон
управления получим в виде:
![]() , где k –
настраиваемый коэффициент регулятора. После подстановки закона управления в
уравнение объекта управления получим уравнение обобщенного настраиваемого
объекта
, где k –
настраиваемый коэффициент регулятора. После подстановки закона управления в
уравнение объекта управления получим уравнение обобщенного настраиваемого
объекта
![]() .
.
Достижение
поставленной цели управления можно анализировать с помощью функции цели ![]() , если
, если ![]() при
при ![]() , то
, то ![]() , что и
требуется по условию задачи. В соответствии с градиентным методом алгоритм
адаптации запишем в виде
, что и
требуется по условию задачи. В соответствии с градиентным методом алгоритм
адаптации запишем в виде
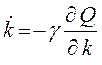 или
или 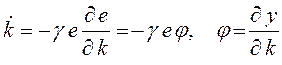 ,
,
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.