Системы прямого адаптивного управления: Учебное пособие по курсу “Адаптивные системы управления”, страница 21

                                       (4.42)

производная которой  в силу уравнений системы (4.41) имеет вид:        

Пусть выполняется равенство тогда  

                      

Как и в предыдущем случае примем , в результате чего имеем

                                   (4.43)

Потребуем выполнения равенства

оно достигается, если l_i  удовлетворяют условию

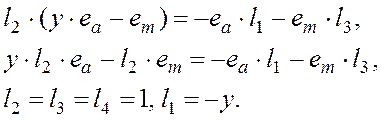                                                               (4.44) 

Подставим  l_i  из (4.44) в (4.41) и (4.43),  тогда релейный  алгоритм настройки коэффициентов запишется в виде

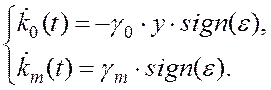                                                                            (4.45)         

 а производная исследуемой функции -

                                                                               

Отсюда следует, что требование отрицательной определенности производной выбранной функции  выполняется, если коэффициенты передачи адаптора выбирать из условия (4.39).

Далее рассмотрим функцию в виде квадратичной формы относительно координатного рассогласования

                                                                                                             (4.46)

Производная данной функции с учетом выражения

и алгоритма адаптации (4.41) определяется следующим образом

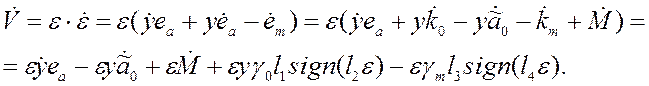
Для упрощения исследования примем  тогда

С помощью l_iобеспечим выполнение равенства

                                                                                                              

то есть

                                                                                  (4.47)

Учитывая полученные условия (4.47), полная производная исследуемой функции приводится к следующему виду:

                               (4.48)

Допустим справедливо соотношение норм функций  тогда для доминирования знакоопределенной составляющей выражения  (4.48) необходимо, чтобы коэффициенты алгоритма адаптации удовлетворяли  условию (4.39).

            В результате релейный алгоритм адаптации, полученный с помощью функции (4.46) имеет вид

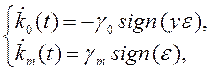                                            (4.49)

Сравнивая вид алгоритмов (4.45) и (4.49), можно заметить, что вид функции V повлиял только на алгоритм параметрической настройки.

Таким образом, сходимость процессов в адаптивной системе пониженного порядка обеспечивается, если выполняются условия (4.38), (4.39) для системы с «гладким» алгоритмом адаптации и соответственно условия (4.39), (4.44) или (4.47) – для системы с релейным алгоритмом адаптации. Следует отметить, что для всех рассмотренных видов адаптивных систем необходимо, чтобы темп изменения коэффициентов регулятора был выше темпа возмущений. Поэтому алгоритмы адаптации, синтезированные на основе принципа локализации, в отличие от алгоритмов, рассмотренных в разделе 3, можно назвать быстрыми.

ПРИЛОЖЕНИЕ 1

          Пусть  функция имеет производные любого порядка в окрестности точки t₀ . Для такой функции можно найти многочлен следующего вида:

                         

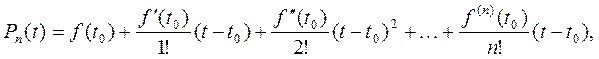
Обозначим через разность значений данной функции f и многочлена

                                                                                                

откуда

                                                                                               

или в развернутом виде

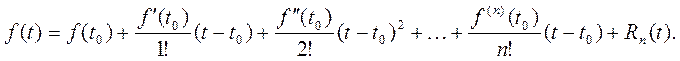        (П1)

Ряд (П1) называется рядом Тейлора функции fпо степеням   а – остаточным членом этого ряда.  Для тех значений t, для которых остаточный член мал, многочлен  дает приближенное представление функции  Правомерность разложения непрерывной функции в ряд Тейлора подтверждает следующая теорема.

          Теорема: Если функция  fимеет на отрезке  производные любого порядка и остаточный член ряда Тейлора стремиться к нулю при

                                                                            

на этом отрезке, то  fразлагается в сходящийся к ней ряд Тейлора на этом отрезке.