1) вторым методом Ляпунова. Алгоритм адаптации получается из условия устойчивости замкнутой системы. Функция Ляпунова обычно выбирается в виде суммы целевого функционала и квадратичной формы от рассогласования между настраиваемыми и идеальными параметрами.
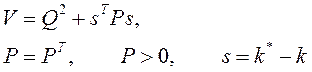
k* - идеальные значения параметров, k- настраиваемые коэффициенты;
2) градиентным методом. Алгоритм адаптации строится в направлении антиградиента целевой функции по рассогласованию или настраиваемым коэффициентам. Алгоритм настройки коэффициентов зависит от функции чувствительности, в которую входят неизвестные параметры объекта управления. Поэтому используют приближенные методы вычисления функции чувствительности;
3) методом скоростного градиента. Изменение коэффициентов осуществляется в направлении антиградиента производной целевой функции по настраиваемым коэффициентам. В результате не требуется определения функции чувствительности;
4) методами, основанными на теории гиперустойчивости. Синтез алгоритма адаптации осуществляется из условия гиперустойчивости замкнутой системы;
5) методами, основанными на организации скользящих режимов;
6) методом мажорирующих функций и т.д.
В классической теории автоматического управления цель функционирования системы задаётся, как правило, некоторым предельным соотношением и набором желаемых показателей качества процессов таких, как время переходного процесса (tп), перерегулирование (s), колебательность (m), установившаяся ошибка (еуст) и т.д. Наряду с перечисленными прямыми показателями существуют обобщённые, в частном случае, интегральные показатели качества:
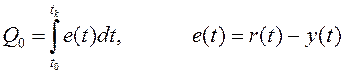
r(t) – эталонный входной сигнал системы; y(t) – выходной сигнал системы; t0, tk – начальный и конечный моменты времени.
В адаптивных системах цель управления или цель функционирования системы управления задаётся в виде набора обобщённых показателей качества,
Q = Q (x, u, t),
x, u – векторы координат состояния и управляющих воздействий соответственно.
Задача состоит в определении управляющих воздействий
![]()
как функции времени в интервале t0 ≤ t ≤ tk и координат состояния, минимизирующих или максимизирующих заданный критерий – функционал (критерий качества). Например,
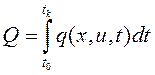
и удовлетворяющих неравенству
J ( u) ≤ 0,
которое определяет область допустимых управлений U.
Критерий качества часто называют целевым критерием, а функционал качества Q(.) – целевым функционалом. Различают
а) локальный целевой функционал
Q=Q(x,u,t), где Q(x,u,t) – скалярная функция,
б) интегральный целевой функционал
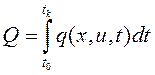
где q(.) – скалярная функция.
В ряде случаев целевой функционал имеет вид квадратичной формы и используется в процессе расчёта системы как функция Ляпунова.
Пример 2.1. Приведем несколько примеров локальных целевых функционалов.
1. Q = eT He,
где е = х* - х (х* - предписанное значение вектора координат состояния )
или е = r(t) – y(t).
2. Q = eT He,
где
e = F-![]() (F – вектор – функция, задающая желаемые динамические
свойства системы).
(F – вектор – функция, задающая желаемые динамические
свойства системы).
Критерий качества или целевые критерии могут задаваться в виде предельных неравенств
![]() ,
,
здесь d - допущенное значение целевого функционала, в частном случае d=0 , тогда
![]() .
.
Иногда критерии качества формулируются в виде асимптотических соотношений, например, Q→ 0 при t→ ¥.
Замечание: числовая (действительная или комплексная) функция, определённая на некотором множестве функций, называется функционалом. Сами преобразования (функции, операции) можно рассматривать как новые математические объекты.
Следует помнить, что целевые критерии, как правило, имеют физический или геометрический смысл. Они могут формулироваться как допустимый минимум некоторой меры отклонения системы от желаемого или предписанного состояния или минимум энергетических затрат на отработку возмущающего воздействия и т.д.
3. Методы синтеза непрерывных адаптивных систем
3.1 Метод большого коэффициента
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.