Системы прямого адаптивного управления: Учебное пособие по курсу “Адаптивные системы управления”, страница 5

неопределённость математической модели ОУ,

неопределённость характеристик среды функционирования,

неопределённость целевого условия.

Рассмотренные источнииы неопределённостей можно иллюстрировать следующим рисунком 1.4.

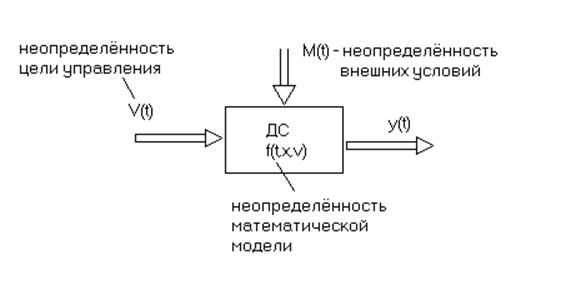
Рисунок 1.4

На рисунке 1.4 использованы обозначения: ДС – динамическая система,  f(.) – математическая модель системы,

V (t) – вектор входных воздействий, M (t) – вектор возмущающих воздействий, y (t) – вектор выходных переменных.

Отметим, что регулятор, обеспечивающий устойчивость системы, может обеспечить заданную точность только при ограниченном диапазоне вариаций характеристик ОУ и условий его функционирования.

1.5.2  Виды неопределённостей

Параметрическая неопределённость

Данный вид неопределённостей означает зависимость свойств (характеристик) ОУ от неизвестных параметров (массы, момента инерции, коэффициента жесткости и т д). Параметры могут быть неизвестными постоянными или медленно меняющимися по сравнению с другими процессами в замкнутой системе. Принято соотносить темп изменения параметров с темпом переходного процесса или темпом изменения переменных состояния объекта.

          Если параметры изменяются медленно по сравнению с изменением состояния объекта (x(t)), то в изменениях переменных состояния накапливается достаточно информации о дрейфе параметров.

Предположение о медленном изменении неизвестных параметров называется гипотезой квазистационарности. Практически это означает, что параметры объекта считаются постоянными или «замороженными». При этом объект также называется квазистационарным или «объектом с замороженными коэффициентами».

Параметры могут быть неизвестными и переменными. Темп их изменения сравним с темпом процессов в объекте управления или темпом изменения внешних воздействий. Параметрическая неопределённость может быть априорной или текущей. Динамические системы с таким видом параметрической неопределённости называются нестационарными.

Случай параметрической неопределённости объекта является наиболее изученным в теории адаптивного управления.

          Пример 1.1. В безредукторном электроприводе вал двигателя непосредственно соединён с нагрузкой. Такая схема применяется, например, в мехатронных поворотных столах. При отсутствии редуктора уравнение вращающихся масс электропривода (без учёта внешнего возмущающего момента) имеет вид:

                                                                                                                                                                                                                                (1.1)

где j - угол поворота вала, Jg– момент инерции якоря электродвигателя,  Jн – момент инерции нагрузки, kс – коэффициент скоростного трения,     Мg- вращающий момент. Обычно Jн>> Jg, кроме того, во многих практических случаях Jн заранее точно не известен. Как правило, задаются только диапазоном возможных значений Jн :

Jн min ≤ Jн ≤ Jн max.

Если диапазон значений достаточно широк, то модель (1.1) считается априорно параметрически неопределённой.    Введём обозначения в уравнение (1.1):

y= j,   u= Mg ,  a20= Jg,   a21(t)= Jн.

C учётом принятых обозначений исходноу уравнение примет вид

                                                           .

Если (а₂₀ + а₂₁(t)) ¹ 0 ( для 0≤ t<¥) , то можно преобразовать полученное уравнение, т.е.                                                              ,

       где                         

Коэффициенты а̃₁(t), b̃(t) характеризуют параметрическую неопределённость.

Неопределённость внешних условий

Значительное влияние на поведение реальных систем управления оказывает окружающая среда (влажность, температура, скорость движения воздушных масс, характеристики нагрузки и т.д.) Неопределённость внешних условий учитывается в математической модели в виде возмущающих воздействий и (или) сигналов задания.