Системы прямого адаптивного управления: Учебное пособие по курсу “Адаптивные системы управления”, страница 7

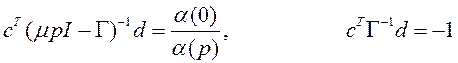
где a(р) – гурвицев полином,  р=d/dt. Тогда при m= 0  имеем

Если m обращается в ноль, то изменяется структура системы (1.3),(1.4). Поэтому используется термин «структурные возмущения». Но из-за того, что меняется порядок системы, такие возмущения называют также сингулярными, а система (1.3), (1.4) – сингулярно возмущенной.

2. Задача синтеза непрерывных адаптивных систем

2.1 Постановка задачи адаптивного управления

          Динамическая система, состоянием которой требуется управлять, описывается уравнениями состояния

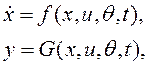                                                                                                   (2.1)

где хÎRⁿ , yÎR^l , uÎR^m , θÎR^s - векторы переменных состояния, выходных переменных, управляющих воздействий, параметрических возмущений (рисунок 2.1).

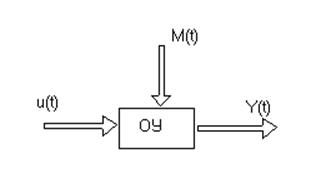
Рисунок 2.1

          В уравнении (2.1) помимо объекта управления могут входить математические модели исполнительных, измерительных устройств. Вектор – функции f, G предполагаются известными, но зависимость f и G от параметра времени t отражает некоторую неопределённость по параметрам и внешним условиям. В реальных условиях параметрические и аддитивные возмущения ограничены, поэтому учитывается ограничение на уровень возмущений

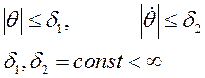                                               (2.2)

          В простейшем случае цель управления задаётся в виде неравенства

                                                    ,                                        (2.3)

гдеQ – целевая функция, δ_q – допустимое значение целевой функции.

          Желаемое поведение системы может быть задано с помощью эталонной модели

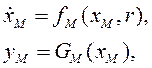                                             (2.4)

гдеx_мÎRⁿ – вектор состояния модели, y_мÎR^l – вектор выходных переменных модели.

          Задача синтеза адаптивной системы управления состоит в определении алгоритма управления

                                                                                 (2.5)

   и алгоритма адаптации

                                                                                    (2.6)

которые обеспечивают достижение поставленной цели (1.7) в системе (2.1), (2.4)-(2.6) для любых возмущений из ограниченного множества (), где W_q- ограниченная область значений q, в которой выполняется неравенство (2.2). В уравнениях (2.5), (2.6)  u_t,  k_t – некоторые операторы.

          Система (2.1), (2.4) - (2.6) называется адаптивной в классе W_q по отношению к цели (2.3), если для любого qÎW_qи при любых начальных условиях x(0), u(0), k(0) выполняется неравенство (2.3).

2.2 Этапы синтеза адаптивной системы

          Адаптивная система (2.1), (2.5), (2.6) имеет двухуровневую схему, поэтому выделяют два основных этапа расчета:

1)  синтез основного контура (2.5),

2)  синтез контура адоптации (2.6).

          К методам синтеза основного контура, получившим наибольшее распространение, относятся:

1)  метод эталонного уравнения (или метод инвариантности). Уравнение закона управления получается из равенства правых частей уравнений эталонной модели и модели объекта управления;

2)  метод модального управления. Закон управления определяется, исходя из желаемых показателей качества переходного процесса;

3)  методы оптимального управления. Закон управления получается в результате решения задачи оптимизации по управляющему воздействию некоторого обобщённого показателя качества;

4)  метод сингулярных возмущений. Для синтеза закона управления используется упрощённая модель системы, которая получается в результате выделения подсистем быстрых и медленных процессов. Закон управления определяется по модели, описывающей подсистему медленных движений.

          В результате применения одного из перечисленных методов получают «идеальный» закон управления. Как правило, вид уравнения основного контура следующий

где k_х,, k_r – матрицы коэффициентов соответствующих размерностей.

          Второй этап синтеза сводится к определению оператора k_t (2.6). Алгоритм настройки коэффициентов регулятора может быть определен