где параметры ![]() имеют
следующие значения:
имеют
следующие значения: ![]() ;
; ![]() ;
; ![]() – входные воздействия. Тогда уравнения замкнутой системы, полученные в
соответствии с изложенной методикой, имеют вид:
– входные воздействия. Тогда уравнения замкнутой системы, полученные в
соответствии с изложенной методикой, имеют вид:
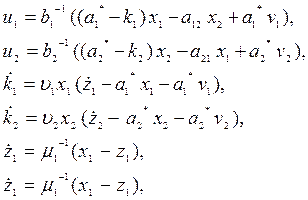 (4.8)
(4.8)
где ai* -
коэффициенты эталонной модели. Структурная схема адаптивной системы (4.8)
изображена на рис. 4.1. На рис. 4.2, 4.3 показаны процессы, наблюдаемые в
системе при постоянных входных сигналах и следующих значениях
параметров системы: ![]() ,
, ![]() , параметрические возмущения заданы вида
, параметрические возмущения заданы вида ![]() . Воздействие на вход системы импульсными
сигналами приводит к процессам, представленным на рис. 4.4 – 4.7. Нетрудно
видеть, что переходные процессы удовлетворяют заданным показателям качества.
При этом наблюдается ограниченное по амплитуде управляющее воздействие в каждом
канале. В начальный момент времени отсутствуют «выбросы» выходных переменных
регулятора, превышающих среднее значение амплитуды колебаний. Разнотемповость
движений хорошо видна по проекции фазового портрета в трехмерном пространстве
(рис. 4.6). Из начальных условий изображающая точка движется вдоль оси s1(
. Воздействие на вход системы импульсными
сигналами приводит к процессам, представленным на рис. 4.4 – 4.7. Нетрудно
видеть, что переходные процессы удовлетворяют заданным показателям качества.
При этом наблюдается ограниченное по амплитуде управляющее воздействие в каждом
канале. В начальный момент времени отсутствуют «выбросы» выходных переменных
регулятора, превышающих среднее значение амплитуды колебаний. Разнотемповость
движений хорошо видна по проекции фазового портрета в трехмерном пространстве
(рис. 4.6). Из начальных условий изображающая точка движется вдоль оси s1(![]() ) при постоянных значениях y1, y2. Затем,
начиная с некоторого момента времени, когда s1 достигнет нулевого значения, изображающая точка
переходит на плоскость (y1,y2).
) при постоянных значениях y1, y2. Затем,
начиная с некоторого момента времени, когда s1 достигнет нулевого значения, изображающая точка
переходит на плоскость (y1,y2).
Ведение нелинейного звена с релейной характеристикой в
адаптор позволяет добиться дополнительных «форсирующих» свойств при ненулевых
начальных условиях в контуре настройки коэффициентов регулятора. Влияние
нелинейного звена иллюстрируется рис. 4.8, 4.9. Сравнение выходных процессов
адапторов позволяет говорить о том, что использование sign(x) приводит к
увеличению амплитуды выходного сигнала в течение первых двух секунд. Это
обусловлено нулевым значением входного воздействия по первому каналу. Так как ![]() , где
, где ![]() , то
функция
, то
функция ![]() остается положительной и равной
остается положительной и равной ![]() . Если производная постоянна, то
. Если производная постоянна, то ![]() , где
, где ![]() –
переменная времени. Следовательно,
–
переменная времени. Следовательно, ![]() является монотонно
возрастающей функцией.
является монотонно
возрастающей функцией.
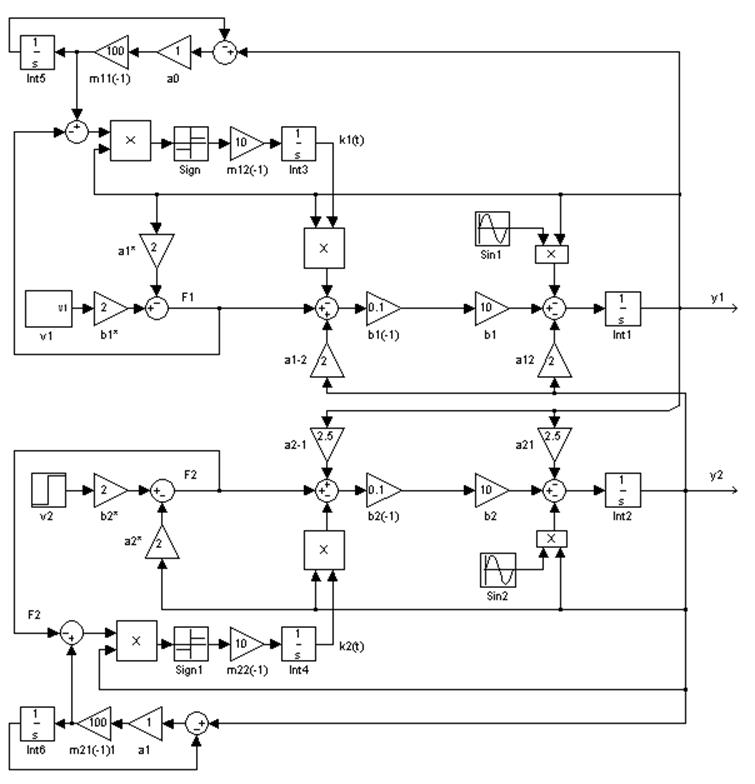 Рисунок 4.1. Структурная схема адаптивной системы
Рисунок 4.1. Структурная схема адаптивной системы
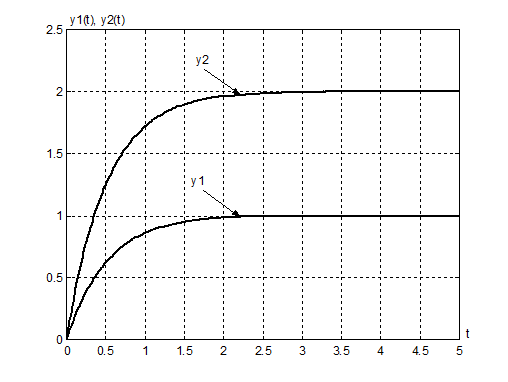
Рисунок 4.2. Выходные процессы при постоянных входных сигналах
|
|
|
|
|
|
|
Рисунок 4.6 Проекция фазового портрета на подпространство (y1, y2, s1) |
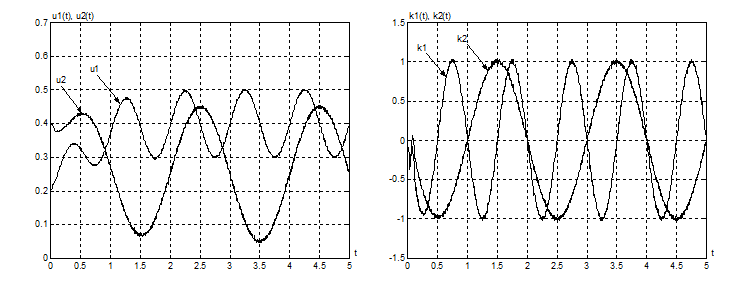
Рисунок 4.7. Процессы в адапторах |
|
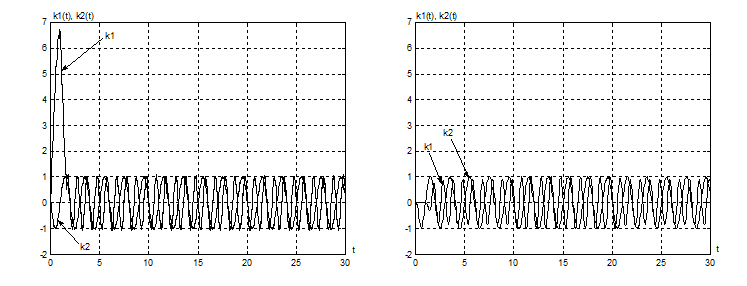
Рисунок 4.8. Выходные процессы адапторов с нелинейным звеном |
Рисунок 4.9. Выходные процессы адапторов без нелинейного звена |
Синтез адаптивного регулятора на основе метода вектора скорости позволил получить качественно новые свойства систем данного класса. Желаемое качество выходных процессов обеспечивается при нулевых начальных условиях. Система сохраняет устойчивость независимо от действующих возмущений, координатных и параметрических начальных рассогласований в системе. Целесообразность использования рассмотренного класса адаптивных систем обусловлена жесткими требованиями к динамическим свойствам систем при существенной нестационарности характеристик объектов управления.
Качество
работы системы в большей степени зависит от амплитуды и в меньшей степени – от
частоты параметрических возмущений. Выбором коэффициентов передачи адаптора
удается выполнить заданные требования по качеству переходных процессов.
Увеличение частоты и (или) амплитуды параметрического возмущения приводит к
необходимости увеличения коэффициента передачи адаптора: ![]() , для гармонических коэффициентов должно
выполняться неравенство:
, для гармонических коэффициентов должно
выполняться неравенство: ![]() .
.
Адаптивная система стабилизации сохраняла устойчивость и при в ведении в объект дополнительных параметрических возмущений (все коэффициенты объекта зависят от времени), при соответствующем выборе коэффициентов передачи адаптора.
Модель линейного одноканального нестационарного объекта управления n-го порядка описывается уравнениями вида:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.