Системы прямого адаптивного управления: Учебное пособие по курсу “Адаптивные системы управления”, страница 11

   Алгоритм настройки коэффициентов согласно (3.1), (3.15), (3.17) имеет вид

или

                                                   (3.18)

   Структурная схема адаптивной системы (3.2), (3.12), (3.18) изображена на рисунке 3.3,

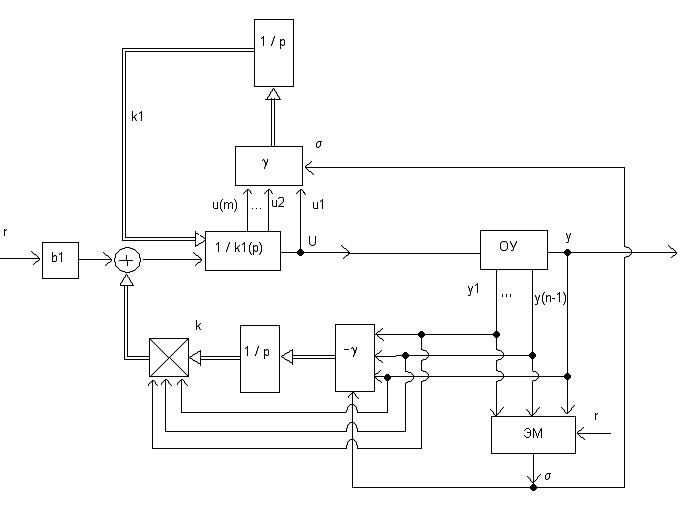
Рисунок 3.3.

где приняты следующие обозначения ,  .

Пример 3.1.

          Выполним расчет адаптивной системы для наиболее простого случая. С этой целью рассмотрим объект управления первого порядка

       ,                                          (3.19)

здесь a₀ (t), b₀ (t) – неизвестные медленноменяющиеся параметры. Процессы в системе должны удовлетворять следующим показателям качества: s% » 0%,         t_n £ 3c, а в установившемся режиме должно выполняться предельное неравенство

   В соответствии с заданными показателями качества определим дифференциальное уравнение эталонной модели

                                                   (3.20)

Согласно (3.12) и (3.18) уравнения регулятора и адаптора имеют вид

                                  (3.21)

   Структурная схема системы с градиентным алгоритмом адаптации имеет вид, изображенный на рисунке 3.4, на котором  принятые обозначения: , .

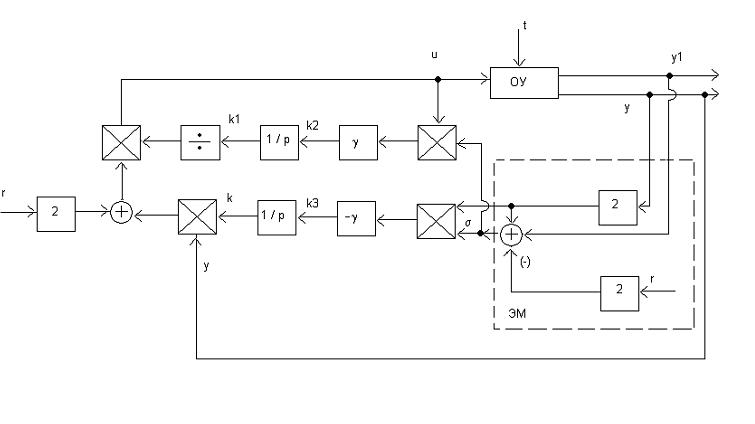
Рисунок 3.4

3.3 Синтез адаптивных систем по схеме скоростного градиента

3.3.1 Общая характеристика схемы скоростного градиента

Суть метода скоростного градиента заключается в следующем: настройка параметров осуществляется в направлении, противоположном скорости изменения целевого функционала вдоль траектории обобщенного настраиваемого объекта .

Идея схемы скоростного градиента принадлежит Красовскому А.А., который для задачи идентификации с адаптивной моделью предложил общий вид алгоритма адаптации, оптимального по критерию обобщенной работы. Алгоритм скоростного градиента (АСГ) нашел дальнейшее развитие в работах А.Л.Фрадкова, Б.Р.Андриевского  и других специалистов в области теории управления.

          Алгоритмом скоростного градиента принято называть правило изменения вектора настраиваемых коэффициентов (q), задаваемое  уравнением вида

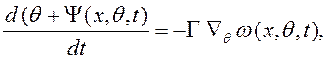                                          (3.22)

где Ñ- дифференциальный оператор, Г = Г ^Т > 0 – квадратная матрица коэффициентов передачи,

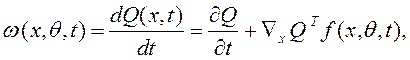
здесь Q(.) – целевой функционал, f (x,q,t) – вектор-функция, описывающая ОНО,

y(.) – вектор-функция, удовлетворяющая условию псевдоградиентности:

Это условие эквивалентно требованию, чтобы угол j между векторами y и w лежал в пределах от - 90⁰ до + 90⁰ (рисунок 3.5).   Условие псевдоградиентности выполняется, если

        или       

(аргументы вектор-функции опущены  для упрощения записи выражений),

   Г_i^T = Г_i > 0 – квадратная матрица коэффициентов (i = 1, 2), Г₂ – диагональная матрица, sign (.) – вектор состоящий из знаков компонент вектора Ñ_q w .

 

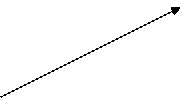                                                 y

                                           j                                  - 90⁰ ≤ j ≤ 90⁰

                                              

                                               Ñ_q w

Рисунок 3.5

   АСГ вида (3.22) называют алгоритмом в конечно-дифференциальной форме. Частными случаями (3.22) являются алгоритмы в дифференциальной форме (при y = 0)

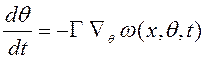                                        (3.23)

и в конечной форме (для Г = 0)

                                         (3.24)

где g - шаг дискретизации.

3.3.2 АСГ в системах с явной реализацией эталонной модели

Рассмотрим пример синтеза системы  с параметрической адаптацией.  Сформулируем задачу синтеза для объекта управления, который задан моделью в пространстве состояний

                                       (3.25)

где xÎRⁿ, uÎR^m – векторы состояния и входа  ОУ,  ,  – матрицы неизвестных коэффициентов соответствующих размерностей,  известно лишь, что значения коэффициентов ограничены по модулю, т.е.

          для всех     i, j, r, p.

    Эталонная модель выбрана в форме

                                     (3.26)

где rÎR^m– задающее воздействие, А_м – гурвицева матрица.