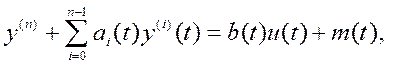Системы прямого адаптивного управления: Учебное пособие по курсу “Адаптивные системы управления”, страница 17

                                                              (4.9)                                       

где y, u – выходная переменная ивходная управляющая переменная соответственно, b(t)≠0 для  начальный и конечный моменты времени. Для неизвестных параметров   и аддитивного возмущения  остаются в силе предположения об ограниченности амплитуды и темпа их изменения, если ввести вектор возмущений ,  то

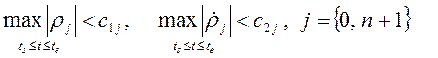   .               (4.10)

Данным условиям удовлетворяет большой класс объектов, например, динамические системы с периодическими коэффициентами, к которым относятся электрические контуры с переменными значениями сопротивлений. Периодическими аддитивными возмущениями могут быть моменты сопротивлений в механической системе с упругими колебаниями или в трехфазном асинхронном двигателе при переменной нагрузке, которая встречается, например, в ленточном конвейере.

          Цель функционирования системы состоит в стабилизации с заданным качеством выходной переменной системы:      .                                         

Рассмотрим  расчет адаптивного регулятора полного порядка на основе метода вектора скорости, а также рассмотрим возможность понижения порядка адаптивного регулятора за счет уменьшения количества контуров адаптации.

4.2.1 Модификации математической модели объекта управления

В адаптивных системах изменение параметров регулятора направлено на подавление возмущений, действующих на объект управления. Поэтому, как правило, число настраиваемых параметров определяется действующими возмущениями.

Уменьшение количества контуров адаптации может являться следствием уменьшения параметрических возмущений, которые учитываются в модели объекта при неизменных условиях его функционирования. Один из способов изменения модели объекта основан на применении ряда Тейлора (Приложение 1). Допустим, что непрерывные функции  имеют производные любого порядка в окрестности рабочей точки и остаточные члены ряда Тейлора стремятся к нулю    ,   , .                         

Разложим параметрические  возмущения  в ряд Тейлора с целью выделения постоянной и переменной составляющей по формуле:

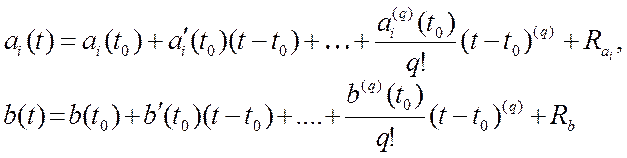                    (4.11)  

где   Выделим в (4.11) первые члены разложения:

                   (4.12)

причем    ,

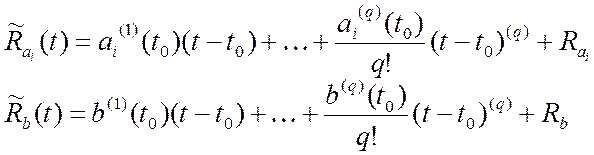
Подставим (4.12) в уравнение объекта (4.9) и приведем исходную модель объекта к виду, в котором в явной форме присутствует стационарная  часть и нестационарная:

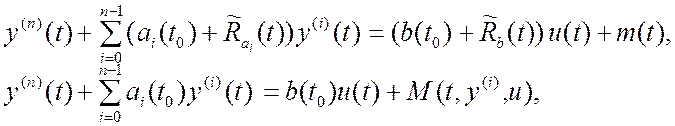            (4.13)

где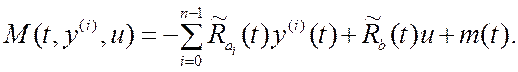                                   

Функция  описывает возмущение, которое по своей природе является структурно-параметрическим, поэтому даже при квазистационарном объекте управления темп возмущения соизмерим с темпом процессов в системе. Следует отметить, что при ограниченных значениях управляющих воздействий, выходных переменных и их производных до (n-1) – порядка можно можно говорить об ограниченности амплитуды и темпа изменения нового возмущения  .  Модель объекта (4.13) будем называть модифицированной 1-го вида.

         На основе разложения в ряд Тейлора непрерывных функций, описывающих возмущения, получим второй вид модели объекта. В данном случае учтем первые два члена ряда   и первые члены ряда разложения , . Согласно (4.11) для  справедливо следующее выражение:

                                                             (4.14)

где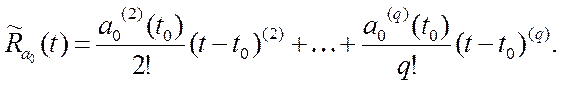 

Введем обозначение

 ,                                                (4.15)

тогда с учетом  (4.12), (4.14) и (4.15) уравнение объекта (4.9) примет вид:

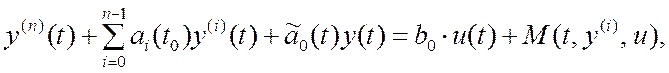       (4.16)   

где – неизвестные значения, представляющие собой либо расчетные номинальные значения, либо априори известные верхние оценки коэффициентов и их производных. Функция

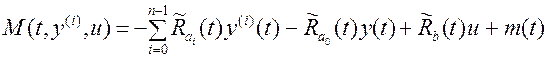, описывает возмущение, которое, как и в первом случае, является структурно-параметрическим.

В модели объекта (4.16) можно выделить параметрическое возмущение  и аддитивное . Модель объекта (4.16) будем называть модифицированной 2-го вида.

4.2.2. Синтез адаптивной системы полного порядка