![]() (4.3)
(4.3)
независимо от действующих возмущений; F - вектор-функция, описывающая желаемые динамические свойства по выходным переменным, v - вектор уставок, v Î Rm, v = const. Решение поставленной задачи стабилизации динамических свойств нестационарного объекта ищется в классе адаптивных систем.
4.1.2 Определение структуры адаптивного регулятора
Нетрудно показать, что для рассматриваемого класса объектов поставленная задача имеет решение, если выполняются условия:
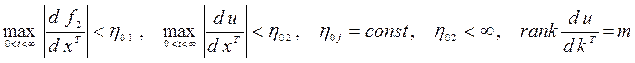
где k - вектор настраиваемых коэффициентов регулятора. Таким образом, дополнительно к условиям, определяющим класс рассматриваемых объектов, требуется ограниченность области допустимых значений переменных состояния, коэффициентов регулятора.
На первом этапе синтеза определяется структура регулятора. Переходные процессы в системе управления должны подчиняться (4.3). Уравнение основного контура получено методом эталонного уравнения (методом разомкнутого контура), т.е. из равенства уравнений замкнутого контура и желаемой динамики:
![]()
![]() (4.4)
(4.4)
где k - вектор настраиваемых коэффициентов регулятора, kÎRm, dim C2=(mxm ), det (C2 B ) ¹ 0. В общем случае алгоритм настройки коэффициентов регулятора можно организовать в соответствии с уравнением
![]()
где Y- нелинейная вектор - функция. В дальнейшем будем рассматривать алгоритмы вида:
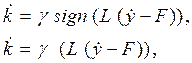 (4.5)
(4.5)
где
g = diag{ g1 ,..., gm } - матрица
коэффициентов передачи, L - вспомогательная матрица, элементы которой
зависят от координат состояния. Значения gj и вид L определяются из условия сходимости
процессов к желаемой траектории. Изменение коэффициента регулятора направлено
на уменьшение рассогласования между ![]() и F.
Использование информации о векторе производных выходных переменных позволяет
говорить о том, что вариации параметров объекта достаточно быстро будут
парироваться коэффициентами регулятора.
и F.
Использование информации о векторе производных выходных переменных позволяет
говорить о том, что вариации параметров объекта достаточно быстро будут
парироваться коэффициентами регулятора.
4.1.3 Сходимость процессов к желаемой траектории
Исследование устойчивости системы с разрывным алгоритмом адаптации проведено на основе аналога теоремы Ляпунова для систем со скользящими режимами [4]. Для анализа системы выбрана функция в виде квадратичной формы
![]() ,
,
где![]() . Полная производная по времени выбранной
функции равна
. Полная производная по времени выбранной
функции равна
![]()
где 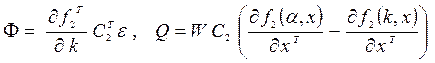 .
.
С
учетом (4.2) производная рассматриваемой функции (![]() )
будет отрицательно определенной, если выполняются условия
)
будет отрицательно определенной, если выполняются условия
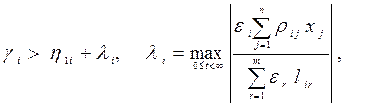 (4.6)
(4.6)
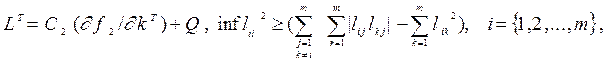 (4.7)
(4.7)
причем
Q = diag{ q j }, Q > 0, Q =
const , а элементы ![]() - зависят от рассогласования между
соответствующими компонентами векторов a и k .
Таким образом, величина λi
определяется, в основном, координатными (εi ) и
параметрическими рассогласованиями.
- зависят от рассогласования между
соответствующими компонентами векторов a и k .
Таким образом, величина λi
определяется, в основном, координатными (εi ) и
параметрическими рассогласованиями.
Утверждение 1: адаптивная система (4.1), (4.4), (4.5) асимптотически устойчива по ε при x ≠ 0, если элементы матриц Lи γ удовлетворяют условиям (4.6), (4.7).
Требуемые
оценки координат состояния и элементов вектора ![]() могут
быть получены с помощью линейного фильтра оценки производных (наблюдателя
состояния) [1,2]. С помощью функций Ляпунова можно получить оценку времени
сходимости процессов к желаемой траектории. Основная идея способа изложена
[5]. В [2] показано, что время сходимости процессов в системе стабилизации с
производными в законе адаптивного управления конечно и зависит от координатных
и параметрических рассогласований в начальный момент времени, а также от
коэффициента передачи адаптора.
могут
быть получены с помощью линейного фильтра оценки производных (наблюдателя
состояния) [1,2]. С помощью функций Ляпунова можно получить оценку времени
сходимости процессов к желаемой траектории. Основная идея способа изложена
[5]. В [2] показано, что время сходимости процессов в системе стабилизации с
производными в законе адаптивного управления конечно и зависит от координатных
и параметрических рассогласований в начальный момент времени, а также от
коэффициента передачи адаптора.
Пример 4.1 Расчет двухканальной адаптивной системы
Рассмотрим свойства адаптивной системы стабилизации динамических характеристик двухканального нестационарного объекта. Динамика объекта описывается уравнениями:
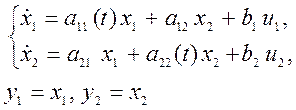
где
![]() - неизвестные переменные, а
- неизвестные переменные, а ![]() -постоянные коэффициенты, i
≠ j.
-постоянные коэффициенты, i
≠ j.
Выбор
желаемой эталонной модели определяется показателями качества (перерегулирование - ![]() , время
переходного процесса по каналам -
, время
переходного процесса по каналам - ![]() , величина
установившейся ошибки -
, величина
установившейся ошибки - ![]() ):
):
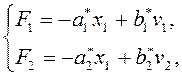
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.