Системы прямого адаптивного управления: Учебное пособие по курсу “Адаптивные системы управления”, страница 20

                                                                   ,   

а полные производные по времени имеют вид

        .                                    

Проверим сходимость  или  с помощью функции вида   которая является положительно определенной, так как

                                                                                          

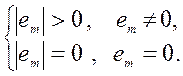
Полная производная рассматриваемой функции равна:

Подставим вместо  соответствующее выражение (4.25)

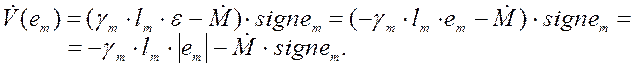          (4.32)

Пусть  вспомогательная функция алгоритма адаптации определяется согласно выражению

                                                               (4.33)

Следует отметить, что вид функции может быть  или, он определяется требованием отрицательной определенности .  Из условия простоты реализации адаптора  выбираем  .  Коэффициент передачи адаптора должен удовлетворять неравенству

                                                                                               (4.34)

где  является ограничением темпа  изменения структурно-параметрического возмущения 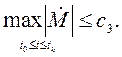 С учетом принятого допущения (4.33) адаптивный закон управления и алгоритм адаптации имеют следующий вид:

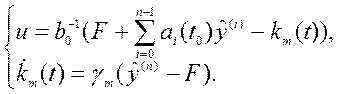
4.2.7 Определение параметров адаптора в системе с двумя контурами настройки

     Алгоритмы настройки коэффициентов, синтезированные  по принципу локализации могут быть двух видов (4.20А), (4.20В). Назовем   алгоритм адаптации (4.20А) «гладким»,  а алгоритм       (4.20В) – релейным. Сначала рассмотрим определение параметров «гладкого» алгоритма адаптации. Запишем уравнение системы с двумя контурами адаптации, подставив в него алгоритм управления:

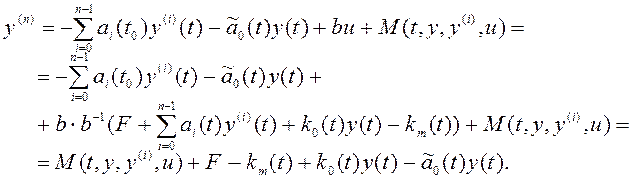                   (4.35)

Учитывая введенные ранее обозначения, запишем уравнение связи между координатными и параметрическими рассогласованиями:

где  является отклонением настраиваемого параметра адаптивного регулятора  от неизвестного параметра объекта   Запишем модель  системы в отклонениях

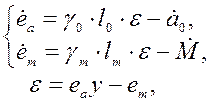                                                                                         (4.36)

так как 

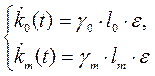
Для проверки сходимости процессов  выберем функцию следующего вида:

                                                                                 

которая является положительно определенной функцией, так как

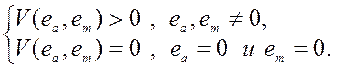
Полная производная выбранной функции равна

                                            .

Преобразуем полученное уравнение

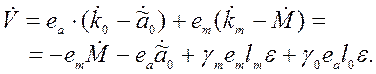                                                             (4.37)

Примем коэффициенты передачи адаптора равными между собой , тогда

                                                 

Если в последнем выражении

,

что будет справедливо, если    или ,

в этом случае   выбираем следующими

                                                                                                    (4.38)

то производная исследуемой  функции будет иметь вид:

                                                                             

Из полученного выражения следует, что при ограниченных по модулю значениях отклонений для отрицательной определенности функции  и соответственно сходимости процессов   необходимо выполнение следующего условия:

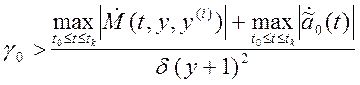                                           ,                     (4.39)

где δ – допустимая динамическая ошибка,  0 < δ << ∞. Выражение (4.39) определяет оценку значений коэффициентов передачи адаптора. С учетом принятых допущений (4.38)  «гладкий» алгоритм адаптации имеет вид

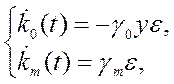                                           (4.40)

в котором значения коэффициентов  выбираются  согласно выражению (4.39).

Перейдем к рассмотрению релейного алгоритма адаптации (4.20В). Известно, что введение релейного элемента  повышает быстродействие адаптора. Представим алгоритм адаптации в следующем виде:

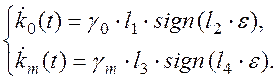                                                                            (4.41)

Задача состоит в определении  и функций l_i . Для ее решения также используем второй метод Ляпунова. Интуитивно понятно, что решение должно зависеть от вида исследуемой функции. Рассмотрим это подробнее. Сначала выберем функцию