Системы прямого адаптивного управления: Учебное пособие по курсу “Адаптивные системы управления”, страница 13

где х ÎRⁿ– вектор состояния, uÎR^m – вектор управления, n ≥ m; A, B – неизвестные матрицы параметров объекта управления, dimA = nxn, dimB = nxm, , .  Коэффициенты матриц А, В заранее не известны. Известно лишь, что значения коэффициентов ограничены сверху и снизу, т.е.

          для всех     i, j, r, p.

Вектор состояния считается доступным измерению, поэтому y = x,  y – вектор выходных переменных.

Желаемая динамика задаётся эталонной моделью вида (3.26)

где х_м ÎRⁿ – вектор состояния эталонной модели, rÎR^m – вектор задающих воздействий. Выбор эталонной модели зависит от требований, предъявляемых к замкнутой системе (времени переходного процесса, перерегулирования, астатизма и т.д.). Эталонная модель должна быть устойчивой, т.е. матрица коэффициентов А_м – гурвицева, поэтому уравнение det (pI – A_м) = 0 имеет все корни с отрицательной вещественной частью, I – единичная матрица соответствующей размерности, В_м – матрица полного ранга.

Цель функционирования системы задана предельным уравнением (3.27)

где e(t) – ошибка системы.

3.4.1. Синтез основного контура

Объект управления (3.25) подвержен действию параметрических возмущений. Поэтому в дальнейшем рассмотрим синтез системы с параметрической адаптацией.

Сначала полагаем, что параметры ОУ известны. Для получения структуры «идеального» регулятора запишем уравнение в отклонениях

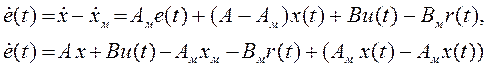                                           (3.43)

Условие разрешимости задачи синтеза согласно (3.43) имеет вид

                                   .                             (3.44)

Разрешая уравнение (3.44) относительно u(t), получим 

домножим слева каждую часть уравнения на B^T

полагаем det (B^TB) ¹ 0 , запишем уравнение «идеального» регулятора

 .                                           (3.45)

Если реализовать управление вида (3.45), то система будет описываться уравнением

Решение этого уравнения равномерно асимптотически устойчиво в силу гурвицевости матрицы А_м. Следовательно, при «идеальном» законе управления (3.45) цель достигается.

Уравнение (3.45) можно записать в виде

                                                  (3.46)

где  -  матрицы идеальных коэффициентов регулятора. Приравнивая коэффициенты в (3.45), (3.46),  найдём соотношение между ними, для коэффициентов при х:

                                                       (3.47)

для коэффициентов при r:

                                                              (3.48)

подставив (3.48) в (3.47), имеем

.                                                  (3.49)

  Условия (3.48), (3.49) называют условиями согласования модели и ОУ.

«Идеальный» закон управления (3.45) или (3.46) не реализуем, так как параметры ОУ не известны. Поэтому выполним замену идеальных коэффициентов регулятора () настраиваемыми (k^r, k^x). Структура регулятора описывается уравнением

.                                         (3.50)

Подставив  (3.50) в модель ОУ, получим уравнение обобщенного настраиваемого объекта

                                              (3.51)

аргумент t опущен для упрощения записи. 

3.4.2. Синтез контура адаптации

На этом этапе расчета системы определяются уравнения,  в соответствии с которыми настраиваются коэффициенты регулятора, т.е. алгоритмы изменения k^r, k^x .  Получим описание обобщенного настраиваемого объекта в отклонениях. Введем обозначения

и подставим (3.50) в (3.43), тогда

  .                                        (3.52)

Введем расширенную матрицу отклонений настраиваемых коэффициентов от их «идеальных» значений

и вектор сенсоров, элементы которого измеряются или вычисляются на основе измерений

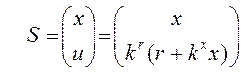       ,     dimS = px 1,   p = n + m.

Уравнение (3.52) примет вид

.

Полученное уравнение является уравнением системы в отклонениях.

Для исследования системы используем функцию, составленную относительно координатных и параметрических рассогласований,

   ,                      (3.53)

где tr (.) – след матрицы (сумма элементов главной диагонали). В силу уравнения (3.52) определим производную функцию V (3.53)