Системы прямого адаптивного управления: Учебное пособие по курсу “Адаптивные системы управления”, страница 14

.

Вторая составляющая уравнения обращается в ноль, если

            (3.54)

Уравнение (3.54) описывает алгоритм адаптации в отклонениях. Производная исследуемой функции принимает вид

отрицательная определенность следует из свойства гурвицевости матрицы коэффициентов эталонной модели и положительности матрицы Н, удовлетворяющей уравнению Ляпунова:

Полагая медленное изменение коэффициентов  и учитывая ранее введенные обозначения, получим вид алгоритмов адаптации:

     ,                                            (3.55)

Структурная схема адаптивной системы (3.25), (3.26), (3.46), (3.55) изображена на рисунке 3.8 . Для обозначения элементов схемы приняты обозначения: .

Условия, при которых решена поставленная задача, являются условиями идентифицируемости  при  и, одновременно, условиями асимптотической устойчивости в целом

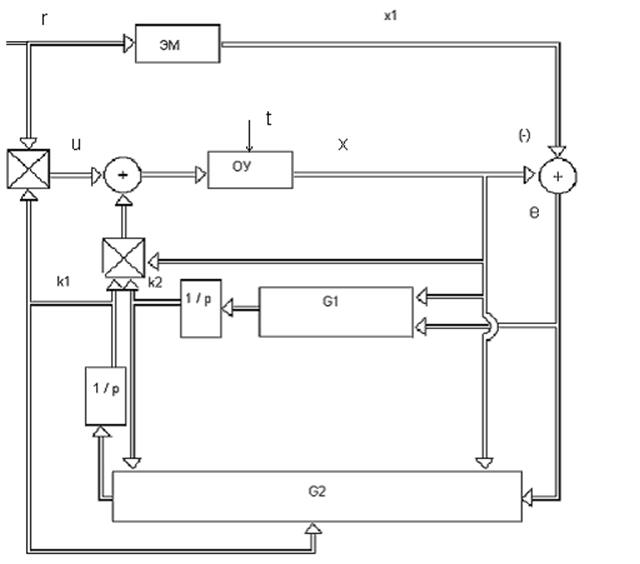
Рисунок 3.8.

Пример 3.3.  Пусть модель объект управления задана уравнением (3.19). Желаемая динамика системы соответствует (3.37). Учитывая координатное рассогласование (3.38), положительно определенная функция  (3.53) имеет вид

при Н = 1, g > 0, а ее производная

так как

Тогда согласно (3.50) и (3.55) уравнения адаптивного регулятора следующие

                                       (3.56)

где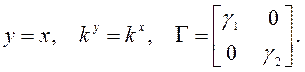

Адаптивная система (3.19), (3.37), (3.56) представлена в виде структурной схемы на рисунке 3.9. На рисунке  приняты следующие обозначения:

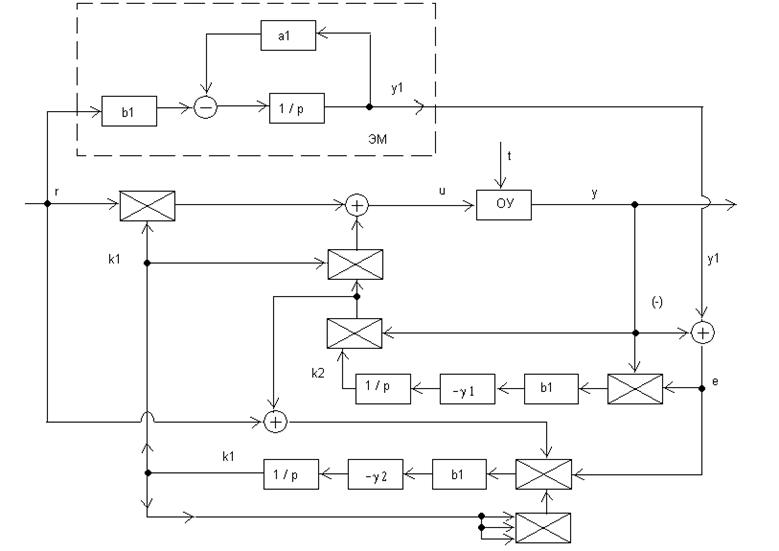
Рисунок 3.9.

4. СИНТЕЗ СИСТЕМ АДАПТИВНОГО УПРАВЛЕНИЯ НА ОСНОВЕ МЕТОДА ВЕКТОРА СКОРОСТИ

4.1 Расчет и анализ свойств многоканальной адаптивной системы

          Стабилизация динамических характеристик систем с  непрерывными нестационарными объектами осуществляется с помощью нелинейного адаптивного регулятора, синтез которого выполнен на основе метода вектора скорости.  В случае одноканальных систем элементы вектора скорости часто совпадают с производными выходной переменной, поэтому применительно к этому классу систем метод можно назвать методом старшей производной. В процессе работы системы собирается и анализируется априори неизвестная информация о свойствах объекта управления. Основным источником такой информации являются производные выходной переменной или вектор первых производных координат состояния. Полученная информация используется в адапторе для изменения значений коэффициентов регулятора. Это позволяет создать «быстрый» адаптор для парирования быстроменяющихся возмущения.  Оценивание требуемых производных осуществляется с помощью малоинерционного линейного фильтра.

4.1.1  Описание задачи

Рассмотрим класс нестационарных нелинейных объектов, модель которых  в пространстве состояний  имеет вид:

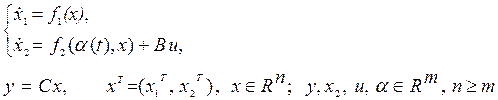                     (4.1)

где y, x, u, a - соответственно векторы выходных переменных, координат состояния, управляющих воздействий, неконтролируемых возмущений, f₁ - известная, ограниченная, непрерывно дифференцируемая вектор - функция, f₂ - взаимооднозначная, непрерывно дифференцируемая по всем аргументам вектор - функция, компоненты которой и частные производные по a, x      ограничены, то есть требуется выполнение условия Липшица. В общем случае f₂  может иметь гладкие нелинейности, но должно выполняться требование линейности по неизвестным параметрам;  С и  В -  известные матрицы коэффициентов,

det (C B) ¹ 0. Априорно известно, что a (t) принадлежит ограниченному нестационарному множеству значений a (t) ÎW^m, в котором  a_j (t) удовлетворяют условию

               (4.2)

где   h _j - известны; причем элементы вектора неконтролируемых возмущений могут  менять знак, что в случае параметрических возмущений приводит к потере устойчивости объекта. Темп неконтролируемых возмущений может быть соизмерим с темпом переходного процесса.

Цель управления состоит в переводе системы из произвольных начальных условий в допустимую ограниченную область, определенную относительно заданного состояния, независимо от действия неконтролируемых возмущений. Перевод объекта из любых начальных условий (y (t₀)) в заданную точку пространства выходных переменных должен осуществляться в соответствии с уравнением