Системы прямого адаптивного управления: Учебное пособие по курсу “Адаптивные системы управления”, страница 19

          Перейдем к рассмотрению модифицированной модели второго вида (4.16)

в которой помимо неизвестной функции M(t) присутствует неизвестный переменный параметр . Таким образом, на  объект действуют   параметрическое и аддитивное возмущения. Согласно последовательности синтеза адаптивной системы, в регулятор необходимо ввести два настраиваемых  коэффициента

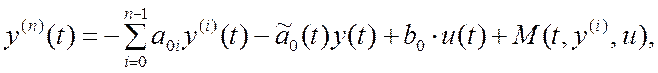
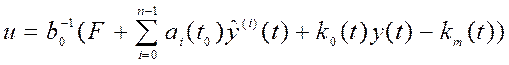          ,                 (4.27)

изменение которых подчиняются алгоритмам  (4.20 А):       

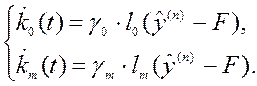                                                            (4.28)

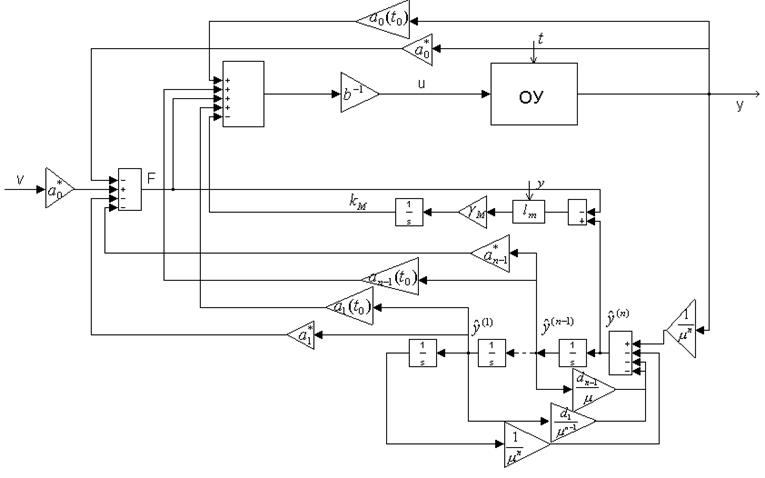
Рисунок 4.10 Структурная схема адаптивной системы с одним контуром адаптации

          Уравнения системы с сигнально-параметрической адаптацией, записанные в расширенном пространстве состояний  имеют вид: 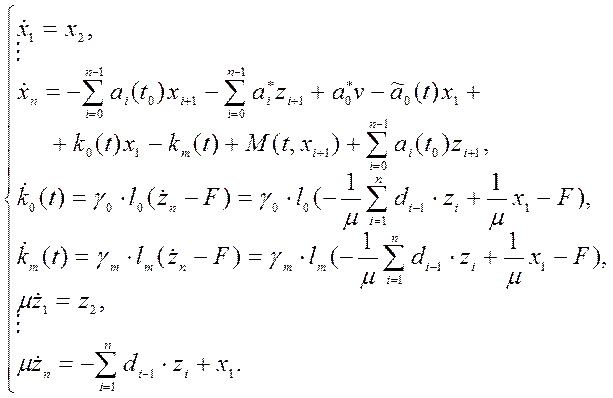        (4.29)

Уравнения (4.29) описывают систему пониженного порядка с сигнально-параметрической адаптацией. Порядок адаптивной системы с двумя контурами адаптации равен  Структурная схема адаптивной системы пониженного порядка (4.29) представлена на рисунке 4.11.

4.2.4  Расчет параметров блока желаемой динамики

Вид переходных процессов в одноканальной стационарной системе определяется расположением корней   характеристического многочлена. Поэтому формирование желаемого дифференциального уравнения связано с заданием корней характеристического многочлена.

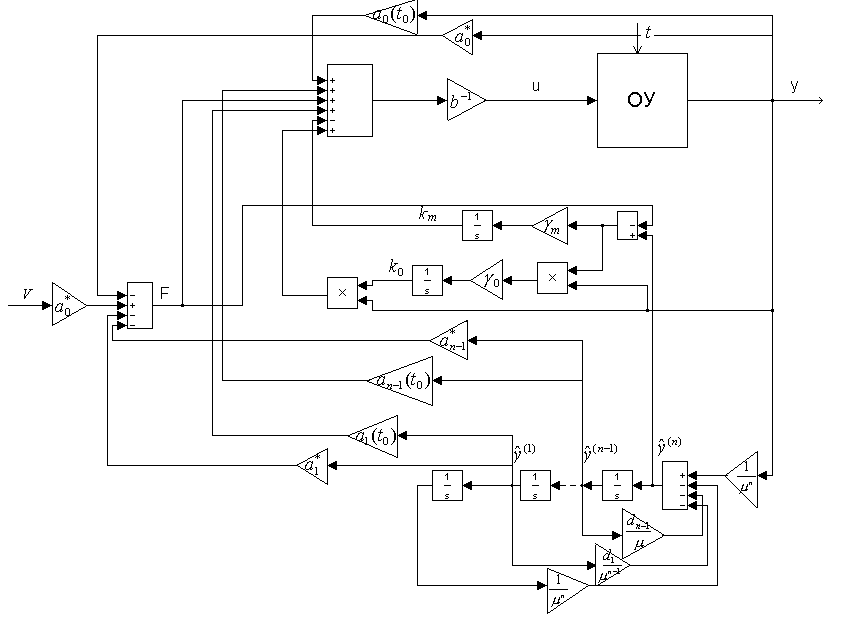
Рисунок 4.11. Структурная схема адаптивной системы с двумя контурами адаптации

Порядок желаемого дифференциального уравнения определяется порядком объекта управления (4.9). Поэтому выбираем n корней  , часть из которых может быть комплексно-сопряженными корнями, и формируем желаемое характеристическое уравнение:

или после раскрытия скобок                                   

                                                       (4.30)    

Согласно (4.30) запишем однородное дифференциальное уравнение:

Так как цель управления заключается в стабилизации выходной переменной системы, то желаемое дифференциальное уравнение системы имеет вид:

4.2.5 Расчет параметров фильтра оценки производных

Реализация выбранного закона управления предполагает введение в систему фильтра оценки производных. Порядок фильтра определяется порядком старшей производной выходной переменной, которая используется в адаптивном законе управления. С целью уменьшения влияния динамики фильтра оценки производных на свойства замкнутой системы его постоянная времени должна быть на порядок меньше минимальной постоянной времени блока желаемой динамики. Таким образом, процессы в фильтре должны быть на порядок быстрее желаемых процессов на выходе системы. 

Так как необходимо оценивать n производных, то дифференциальное уравнение фильтра имеет вид:

                                                  (2.37)

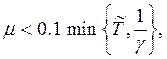
где     – оценка соответственно i-ой производной выходной переменной системы. Степень быстродействия фильтра определяется согласно выражению:     .

4.2.6  Определение коэффициента передачи адаптора в системе с одним контуром настройки

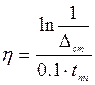Рассмотрим адаптивную систему с одним контуром адаптации вида (4.26). После определения коэффициентов блока желаемой динамики и параметров фильтра, необходимо найти значения коэффициента передачи адаптора. Последняя задача может быть решена с помощью второго метода Ляпунова.  Полагаем, что требуемые оценки производных координат состояний известны точно и  где – ограниченная рабочая область координат состояния.

Введем координатное и параметрическое рассогласования, а затем установим зависимость между. Пусть рассогласование между настаиваемым параметром регулятора  и структурно-параметрическим возмущением  оценивается по выражению

 ,

а отклонение траектории движения системы от желаемой  характеризуется переменной

.

Подставим в уравнение объекта (4.13) закон управления (4.24), в результате получим:

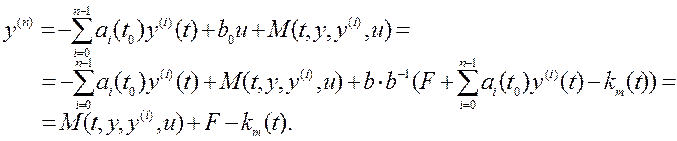           (4.31)

Тогда согласно введенным рассогласованиям и уравнению (4.31) следует справедливость выражения