Системы прямого адаптивного управления: Учебное пособие по курсу “Адаптивные системы управления”, страница 12

Цель управления сформулирована относительно координатного рассогласования

                                              (3.27)

где e(t)=x(t)–x_м(t). Предполагаем выполнение условия управляемости и наблюдаемости координат состояния.

   Пусть целевой функционал выбран в форме скалярной квадратичной функции

                                                 (3.28)

Поставленная цель управления выполняется, если Q®0  при  t®¥.

Синтез адаптивного регулятора начнем с определения уравнения основного контура.    Уравнение основного контура можно получить модальным методом, т.е. разрешив уравнение

относительно u (t):

или                    .                  (3.29)

“Идеальное” управление можно записать в форме

                                                           (3.30)

где матрицы k_*^x, k_*^r удовлетворяют условию

.                                   (3.31)

Матрицы идеальных значений коэффициентов регулятора k_*^x, k_*^r существуют, если выполняются ранговые условия

   Реальный закон управления имеет вид

                                    (3.32)

где k^x (t), k^r (t) – матрицы настраиваемых коэффициентов регулятора, 

   Для определения вида алгоритма адаптации требуется вычислить производную целевого функционала в силу уравнений системы, т.е.

                     (3.33)

После подстановки (3.32) в (3.33) имеем

    (3.34)

Определим скоростные градиенты

  Для алгоритмов настройки коэффициентов выбираем АСГ в дифференциальной форме

                    (3.35)

где Г = gI,  g > 0 .

   Система (3.25), (3.26), (3.32), (3.35) относится к системам с параметрической адаптацией. На основе АСГ можно синтезировать также системы с сигнальной и сигнально-параметрической адаптацией. Структурная схема системы изображена на рисунке 3.6 (использованы обозначения:     f1 = , f2 = ,  x1 = x_м , k1 = k^r ,  k = k^x ,  A1 = B^TH).

   Системы с алгоритмом адаптации (3.35) сохраняют работоспособность при изменении координатных и параметрических возмущений в широких пределах.  Качество процессов ухудшается, если скорость изменения параметрических возмущений высокая.

С целью повышения быстродействия в контурах параметрической настройки коэффициентов регулятора можно применять пропорционально- интегральные алгоритмы адаптации в конечно- дифференциальной форме

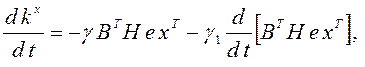
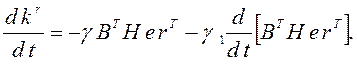                             (3.36)

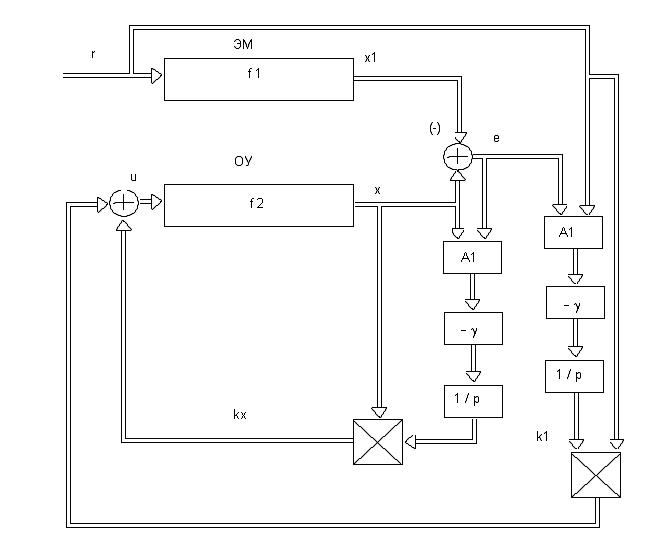
Рисунок 3.6.

Пример 3.2.   Проведем синтез адаптивного регулятора для объекта, рассмотренного в примере 3.1. Уравнение эталонной модели (3.20) запишем в виде

                                                  (3.37)

здесь y_м- выходная переменная b_ом = a_ом = 2,  т.е. эталонная динамика системы формируется динамическим звеном (3.37). Если координатное рассогласование

                                                       (3.38)

то функцию качества (3.28) можно записать следующим образом

                                                      (3.39)

Уравнение регулятора (3.32) с учетом модели объекта (3..37) имеет  вид

                                                 (3.40)

где k^y, k^r - настраиваемые коэффициенты. Тогда полная производная функции (3.39) есть

                              (3.41)

а частные производные функции (3.41) по настраиваемым коэффициентам

.

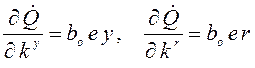Алгоритм настройки коэффициентов регулятора с учетом (3.40) и (3.23) получим в виде

   .                                      (3.42)

Структурная схема системы (3.19), (3.37), (3.40), (3.42) приведена на рисунке 3.7 (использованы  обозначения ).

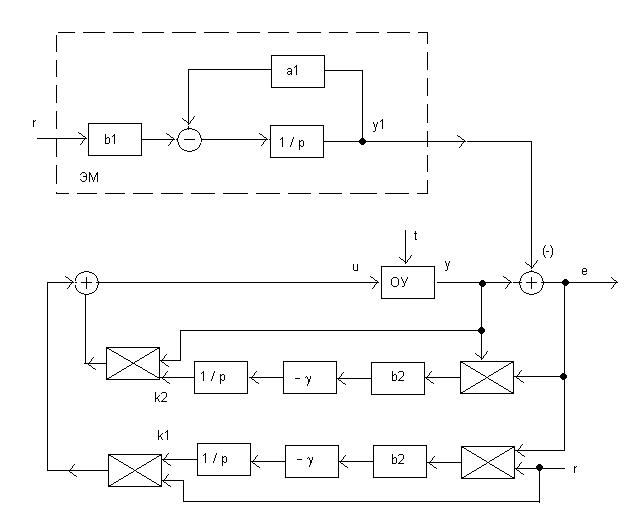
Рисунок 3.7.

3.4 Синтез адаптивных систем методом функций Ляпунова

Второй метод Ляпунова был разработан для исследования устойчивости движения нелинейных систем, которые описываются обыкновенными дифференциальными уравнениями. Впоследствии метод стали использовать для оценивания быстродействия системы. Примерно в 70-е годы прошлого столетия метод нашел применение в задачах синтеза адаптивных регуляторов.

Рассмотрим синтез адаптивных регуляторов методом функций Ляпунова для линейного объекта управления, модель которого имеет вид (3.25)