Использование информационных технологий в анализе, прогнозировании временных рядов и принятии управленческих решений, страница 9

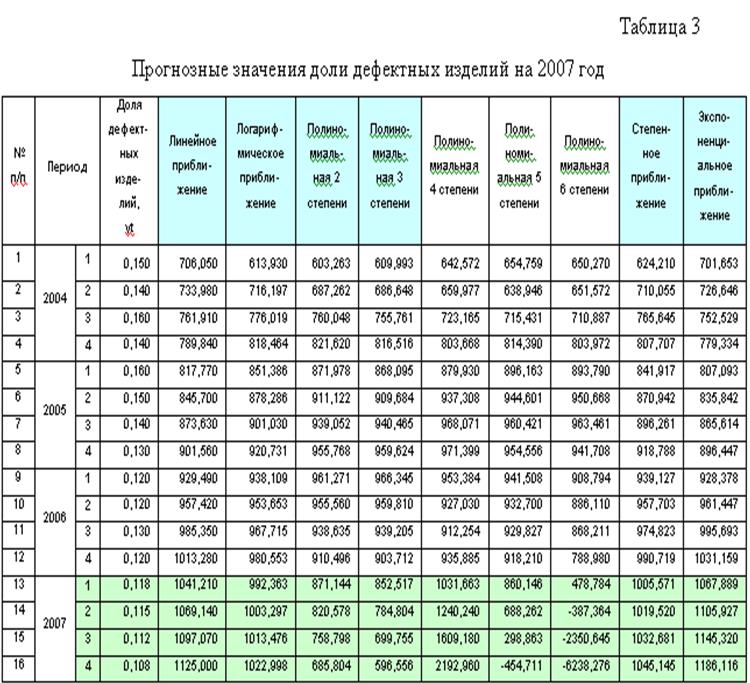
Получение прогнозных значений доли дефектных изделий  на ближайший год по кварталам.Для этого необходимо времен­ной ряд использовать для определения функциональной зависимости развития этого явления. Microsoft Excel предоставляет возможность построения прогнозных значений на базе 9 функций: ли­нейная, полиномиальная (во 2-ой, 3-ей, 4-ой, 5-ой, 6-ой степени), логарифмическая, логарифмическая, экспоненциальная, степенная. Полученные прогнозные значения представлены в таблице 3.

Анализ результатов таблицы 3 показал, что зависимости полиномиальная 4-ой, 5-ой и 6-ой степе­ни не могут быть использованы для дальнейших расчётов, поскольку их прогнозные значения выхо­дят за допустимые, т. е. идут с минусом или имеют большие расхождения.

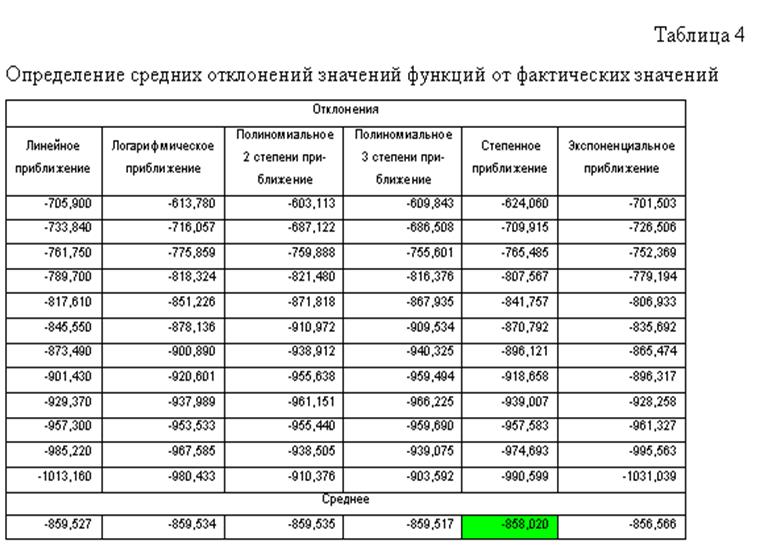
Выбрать для дальнейшего анализа одну зависимостьпозволяют значения, представленные в таб­лице 4. Анализ значений, полученных в таблице 4, позволяет сделать вывод, что для дальнейшего анализа необходимо исполь­зовать степенное приближение, поскольку отклонение степенных значений от фактических наимень­шее (-858,020).

В результате использования степенного приближения, прогнозные значения на ближайший год по кварталам составят: 1005,6, 1019,5,1032,7, 1045,1.

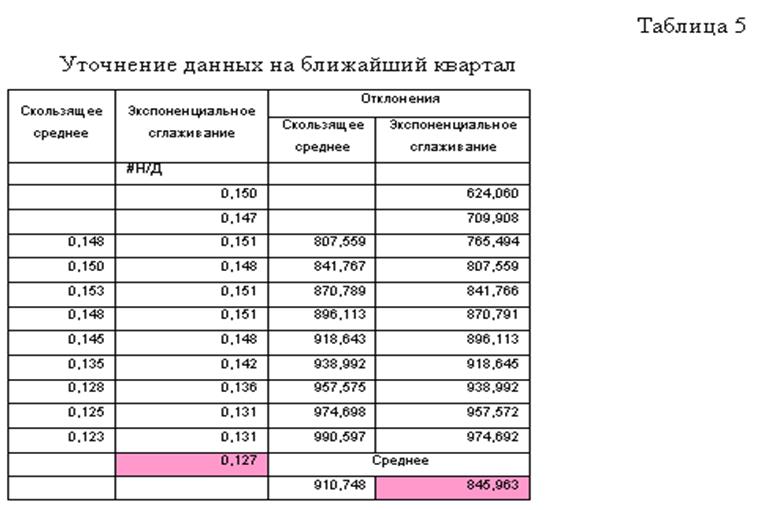
Уточним данные на ближайший квартал.Для этого используем два метода: скользящее среднее и экспоненциальное сглаживание (см. табл. 5). Анализ данных таблицы позволяет сделать вывод, что краткосрочный прогноз должен осуществляться с помощью метода экспоненциальное сглаживание. Т. о. уточнённый краткосрочный прогноз на ближайший квартал составит 0,127.

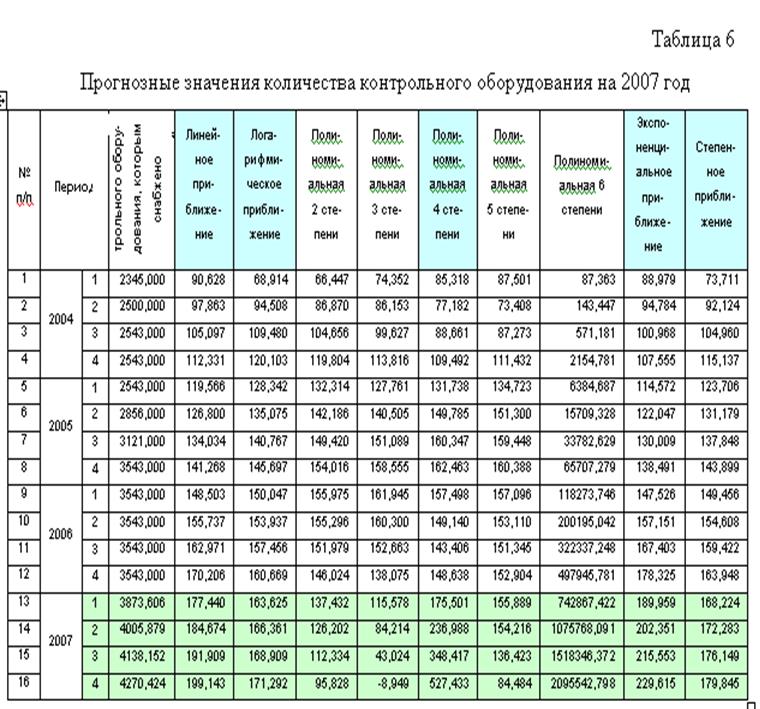
Получение прогнозных значений количества контрольного оборудования  на ближайший год по кварталам.Для этого необходимо времен­ной ряд использовать для определения функциональной зависимости развития этого явления. Microsoft Excel предоставляет возможность построения прогнозных значений на базе 9 функций: ли­нейная, полиномиальная (во 2-ой, 3-ей, 4-ой, 5-ой, 6-ой степени), логарифмическая, логарифмическая, экспоненциальная, степенная. Полученные прогнозные значения представлены в таблице 6.

Анализ результатов таблицы 6 показал, что зависимости полиномиальная 2-ой, 3-ей, 5-ой и 6-ой степе­ни не могут быть использованы для дальнейших расчётов, поскольку их прогнозные значения выхо­дят за допустимые, т. е. идут с минусом или имеют большие расхождения.

Выбрать для дальнейшего анализа одну зависимостьпозволяют значения, представленные в таб­лице 7. Анализ значений, полученных в таблице 7, позволяет сделать вывод, что для дальнейшего анализа необходимо исполь­зовать линейное приближение, поскольку отклонение линейных значений от фактических наимень­шее (2983,250).

В результате использования линейного приближения, прогнозные значения на ближайший год по кварталам составят: 177,440, 184,674, 191,909, 199,143.

Уточним данные на ближайший квартал.Для этого используем два метода: скользящее среднее и экспоненциальное сглаживание (см. табл. 8). Анализ данных таблицы позволяет сделать вывод, что краткосрочный прогноз должен осуществляться с помощью метода экспоненциальное сглаживание. Т. о. 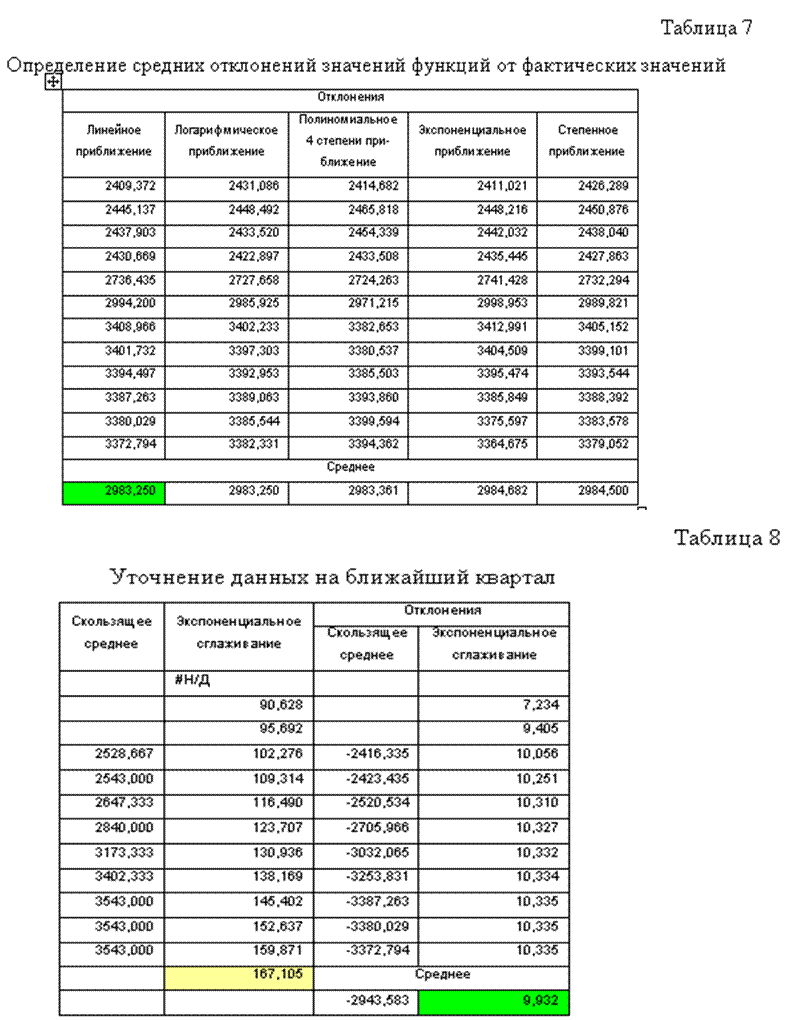уточнённый краткосрочный прогноз на ближайший квартал составит 167,105.

Проанализируем динамику доли дефектных изделий с помощью графиков, представленных на рис. 1 и 2.

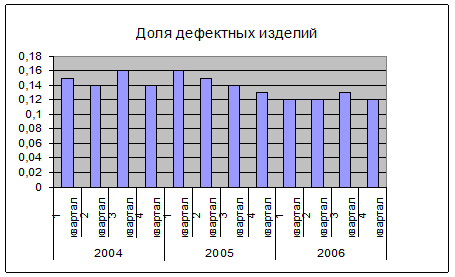
Рис. 1. Динамика изменения доли дефектных изделий по годам

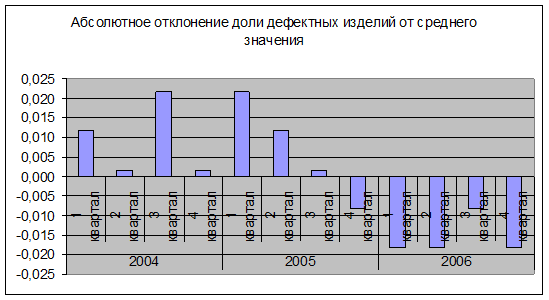
Рис. 2. Анализ абсолютных отклонений доли дефектных изделий от среднего значения

Проанализируем динамику доли дефектных изделий с помощью графиков, представленных на рис. 1 и 2.

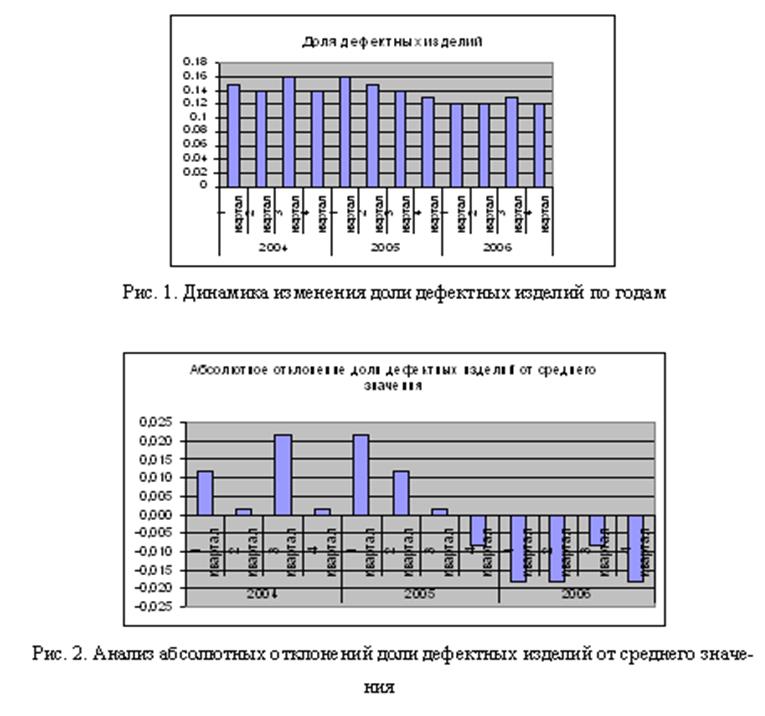
Из рисунка 1 видно, что в течение 2004-2006 годов доля дефектных изделий постепенно уменьшается. С 1 квартала 2004 года по 1 квартал 2005 года наблюдаются небольшие скачки, начиная со 2 квартала 2005 года и до 1 квартала 2006 года доля дефектных изделий уменьшается и далее до конца года остаётся постоянной, только в 3 квартале 2006 года немного возрастает и затем вновь стабилизируется.