- Residuals (Остатки).
 Данные этой области
результатов регрессионного анализа в полном объеме представлена на рис. 6, а
график остатков - на
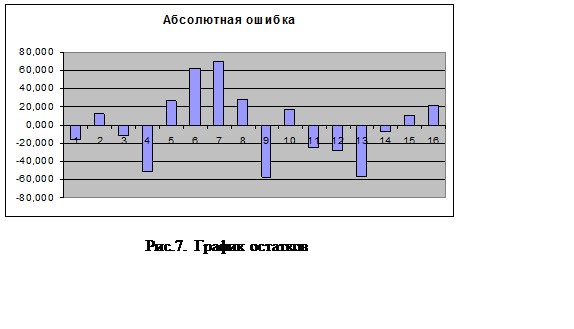
рис. 7. Анализ графика позволяет сделать следующий вывод: за анализируемый
период зафиксировано два выброса - в 4-ом и 9-ом наблюдении. Для дальнейшего анализа значения
выбросов могут быть цензурированы. Если этот процесс осуществляется, необходимо
выполнить регрессионный анализ заново.
Данные этой области
результатов регрессионного анализа в полном объеме представлена на рис. 6, а
график остатков - на
рис. 7. Анализ графика позволяет сделать следующий вывод: за анализируемый
период зафиксировано два выброса - в 4-ом и 9-ом наблюдении. Для дальнейшего анализа значения
выбросов могут быть цензурированы. Если этот процесс осуществляется, необходимо
выполнить регрессионный анализ заново.
3. Анализ качества модели. Для оценки качественности выбранной модели воспользуемся рассчитанными значениями коэффициентов множественной корреляции MultipleR(значение ячейки B4), коэффициента детерминации SquareR2(значение ячейки B5) и AdjustedRSquare(значение ячейки B6).
Коэффициент множественной корреляции R=0,927, что свидетельствует о тесной связи факторов и результативного показателя.
Коэффициент
регрессии R2=0,859 и пересчитанное значение этого
коэффициента с учетом количества используемых факторов модели ![]() =0,837 также подтверждает ее
качество, т.к. в модели 86% или 84% вариации объема реализации продукции
соответственно учтено и обусловлено влиянием включенных факторов.
=0,837 также подтверждает ее
качество, т.к. в модели 86% или 84% вариации объема реализации продукции
соответственно учтено и обусловлено влиянием включенных факторов.
КОЭФФИЦИЕНТНЫЙ АНАЛИЗ
Цель - оценка влияния отдельных факторов регрессионной модели на величину результативного показателя Y.
Инструментарий - встроенные функции MS Excel, таблицы расчетов значений коэффициентов парной корреляции; пакет Анализ данных MSExcel.
Основные положения.
1. При оценке влияния факторов Xна зависимый показатель Yкоэффициенты модели, полученные на этапе регрессионного анализа, играют важную роль. Однако они не позволяют выявить степень влияния каждого фактора xjÎX (j=1,2,…,m) на показатель Yв силу различия единиц измерения и разной степени колеблемости. Для устранения таких различий при интерпретации полученной модели используются средние частные коэффициенты эластичности Э(j) и бета-коэффициенты b(j).
Коэффициент эластичности
![]()
показывает, на сколько процентов изменится зависимая величина показателя Yпри изменении фактора xj на 1%. Однако он не учитывает степень колеблемости факторов.
Бета-коэффициент
![]() ,
,
где ![]() - среднее квадратическое отклонение
зависимой величины Y
- среднее квадратическое отклонение
зависимой величины Y
![]() - среднее квадратическое отклонение фактора xj
- среднее квадратическое отклонение фактора xj
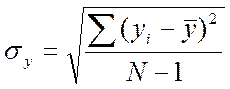
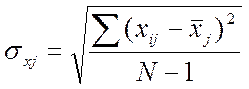
позволяет определить, на какую часть
величины среднего квадратического отклонения ![]() изменится
зависимая величина Y
с изменением соответствующей независимой переменной xj на величину своего среднего
квадратического отклонения
изменится
зависимая величина Y
с изменением соответствующей независимой переменной xj на величину своего среднего
квадратического отклонения ![]() при фиксированном
значении остальных независимых переменных.
при фиксированном
значении остальных независимых переменных.
Для расчета абсолютной величины изменения показателя Yот изменения величины фактора xj используется формула
![]()
2. Указанные коэффициенты позволяют проранжировать факторы X по их степени влияния на зависимую величину Y. Долю влияния каждого фактора xjв суммарном влиянии всех факторов X оценивают по величине дельта-коэффициентов D(j):
![]() ,
,
где ryj-коэффициент парной корреляции между фактором xj(j=1,…,m) и зависимой величиной Y;
R2-коэффициент детерминации.
Задача. Оценить влияние факторов «Расходы на рекламу» (X1) и «Индекс потребительских расходов» (X2) на величину показателя «Объем реализации продукции» (Y) с помощью выявленной на этапе регрессионного анализа модели.
Решение:
1. На отдельный листе MSExcel скопируем исходные данные об объемах реализации, расходах на рекламу и величине индекса потребительских расходов и значения вектора параметров модели: коэффициенты (см. рис. 8).
2. С помощью встроенных функций MSExcel
=СРЗНАЧ()
= КВАДРОТКЛ()
=КОРЕНЬ()
соответственно рассчитываются средние значения, квадратические отклонения и средние квадратические отклонения зависимой величины «Объем реализации продукции» (Y), а также факторов Расходы на рекламу» (X1) и «Индекс потребительских расходов» (X2).
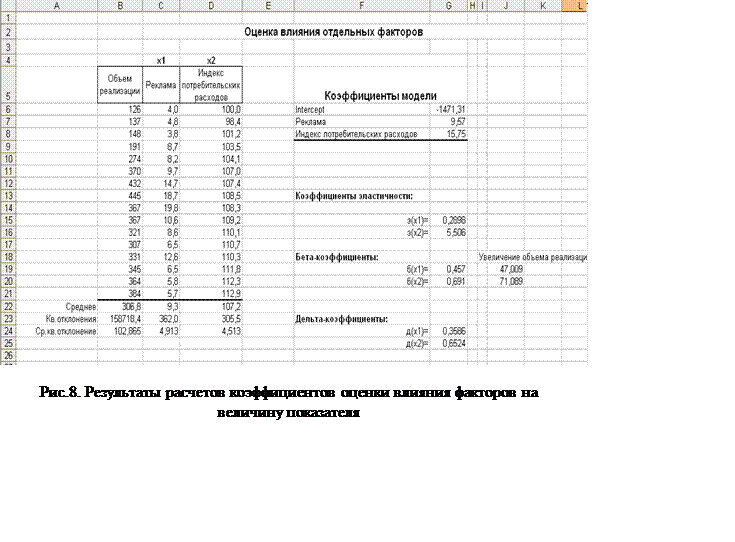
Для показателя Y эти расчеты представлены в виде следующих формул
B22 ® =СРЗНАЧ(B6:B21)
B23 ® =КВАДРОТКЛ(B6:B21)
B24 ® =КОРЕНЬ(B23/(16-1))
3. Расчет значений коэффициентов эластичности:
F15 ®=G7*C22/B22
F16 ® =G8*D22/B22
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.