Использование информационных технологий в анализе, прогнозировании временных рядов и принятии управленческих решений, страница 3

Решение:

1. Формирование матрицы парных коэффициентов корреляции. Расчет коэффициентов парной корреляции будем осуществлять с помощью таблицы, представленной на рис.2.

Для расчета коэффициента корреляции между Объемом реализации продукции (Y) и фактором Время (X1) из таблицы исходных данных были скопированы данные в графы Yи X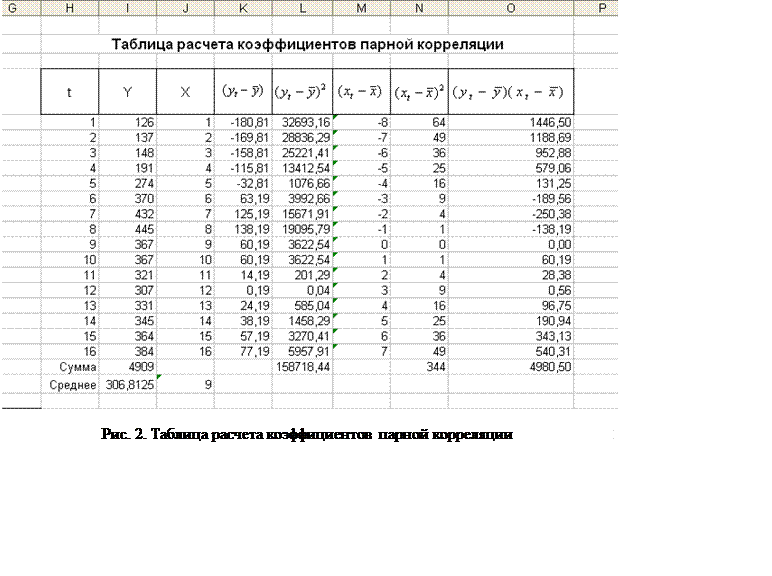соответственно. В последующих графах таблицы введены формулы, представленные в виде заголовков граф. Кроме того вычислены необходимые для расчетов средние и суммарные значения граф таблицы.

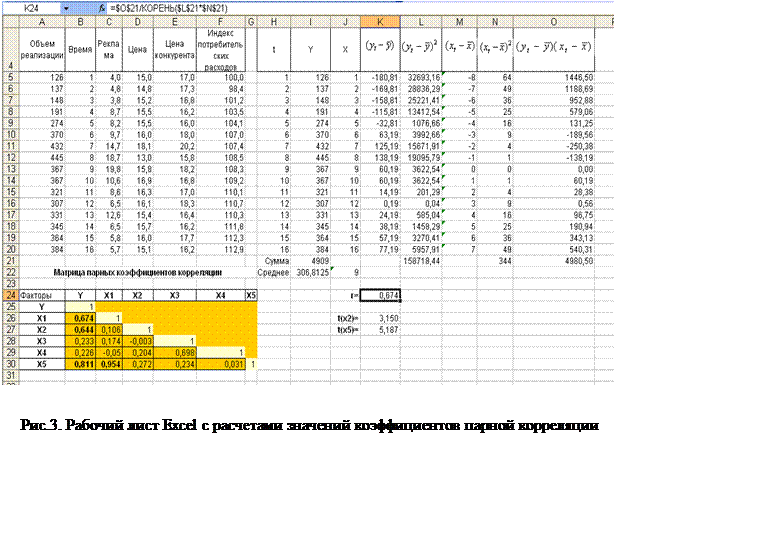
Расчет значения коэффициента корреляции осуществляется в ячейке К24 по формуле =$O$21/КОРЕНЬ($L$21*$N$21). Полученное значение фиксируется в матрице парных коэффициентов корреляции в ячейке B26 (рис.3).

Поочередно заменяя значения графы X  в таблице расчета коэффициентов корреляции исходными данными по остальным факторам, получаем коэффициенты  корреляции показателя Yсо всеми факторами (первый столбец данных матрицы парных коэффициентов корреляции).

Для вычисления значений корреляций между факторами в таблице расчета коэффициентов парной корреляции значения показателя Y заменяются исходными данными первого фактора,  а в графу X - поочередно копируются значения второго и последующих факторов и т.д.

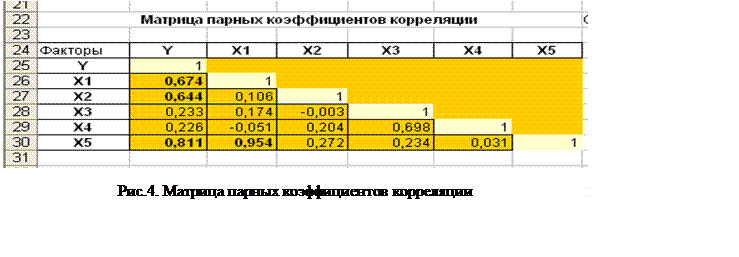В результате будет получена матрица парных коэффициентов корреляции рис.4.

2. Анализ матрицы парных коэффициентов корреляции.

-  Между тремя факторами: Время (х1),  Расходы на рекламу (x2) и Индекс потребительских расходов (x5), - и  Объемом реализации продукции (Y) существует прямая сильная связь (значения коэффициентов корреляции соответственно равны 0,672; 0,644 и 0,811). Два  фактора: Цена товара (x3) и Средняя цена конкурентов (x4), - имеют с анализируемым показателем прямую слабую связь (их корреляция с показателем составляет всего 0,2) и поэтому из дальнейшего анализа исключаются.

-  Между факторами Время (х1) и Индекс потребительских расходов (x5) существует сильная прямая коллениарная зависимость: r_x1x5=0.954. Поскольку фактор Индекс потребительских расходов (x5) с анализируемым показателем Объемом реализации продукции (Y) имеет более сильную связь:

r_yx5(0,811) > r_yx1(0,674), -

для дальнейшего анализа остается именно он.

Таким образом, из пяти факторов имеет смысл оставить только два:  Расходы на рекламу (x2) и Индекс  потребительских расходов (x5).

РЕГРЕССИОННЫЙ АНАЛИЗ

Цель - получение регрессионной модели, т.е. функциональной зависимости результативного показателя Yот значений выбранных факторов.

Инструментарий   -  пакет Анализ данных MSExcel.

Основные положения.

1.  Для отображения зависимости переменных могут использоваться показательная, параболическая и многие другие функции. Однако в практической работе наибольшее распространение получили модели линейной зависимости, когда факторы Xвходят в модель исследуемого показателя Yлинейно.

2.  Коэффициент парной корреляции дает объективную оценку тесноты связи лишь при линейной зависимости переменных. Поэтому, если на этапе построения регрессионной модели была определена иная зависимость, необходимо вернуться к сравнительной оценке и отсеву факторов.

3.  В общем виде линейная модель множественной регрессии имеет следующий вид:

,

где  Y_i -значение показателя Y, рассчитанное в соответствии с  моделью регрессии  для i-ого наблюдения, iÎ[1,N];

x_i1 , x_i2 , … , x_im -значения факторов для i-ого наблюдения;

a₀ ,a₁ ,a₂ , … , a_m-вектор оценочных параметров;

e_i -  значение отклонений (остатков) регрессии от фактического значения показателя Y для i-ого наблюдения.

Формулы расчета  вектора оценочных параметров зависят от количества факторов, используемых в модели. Для оценивания неизвестного вектора параметров пользуются методом наименьших квадратов. Этот метод реализован и в механизме Регрессия пакета Анализ данных MSExcel. 

4.  Значения отклонений (остатков) регрессии от фактических значений показателя Y по всему временному ряду наблюдений используются для проверки качества модели.