Другие предметы \ Теория автоматического управления

Анализ линейных систем автоматического управления: Методическое пособие по дисциплине "Теория автоматического управления", страница 8

Но

Следовательно

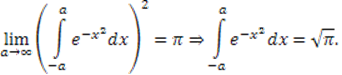
Вернемся к интегралу

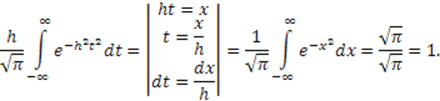
Замечание 1:

Δ – функция, единичная ступенчатая функция и линейно нарастающая функция связанны соответствием

Или

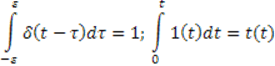
Замечание 2:

Δ – функция четная.

3.3. Импульсная переходная функция.

Импульсной переходной функцией называется функция, которая описывает поведение системы при воздействии на нее дельта функции .

Для того, чтобы убедиться в этом проделаем следующие преобразования:

Пусть поведение САУ описывается линейным дифференциальным уравнением n-го порядка

Если входное воздействие , где – момент приложения дельта - функции, то уравнение (3.3) должно принять вид:

так как есть решение уравнения (3.3). Учтем тот факт, что начальное состояние системы равно нулю, то есть

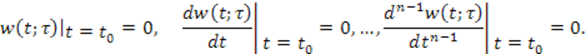
Умножим обе части уравнения (3.3) на и проинтегрируем их по

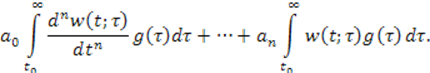
Так как дифференцирование производится по , а интегрирование по , то эти операции можно выполнять в любой последовательности (сначала найти интеграл, а потом производную от полученного результата).

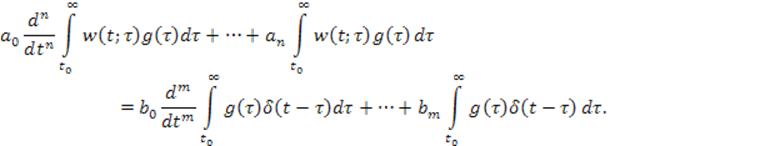
В соответствии со свойством дельта функции

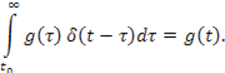
Следовательно

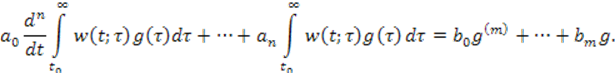
Правые части уравнения (1) и последнего выражения совпадают. Но в этом случае должны совпадать и левые части. Это возможно, если

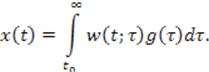
С учетом того, что импульс действует только мгновенно, пределы интегрирования можно уменьшить до текущего значения

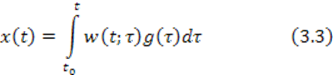
Последнее выражение показывает, что для определения входного состояния системы необходимо импульсную переходную функцию умножить на входное воздействие и полученное произведение проинтегрировать.

Если система стационарная, то (3.3) можно переписать несколько иначе:

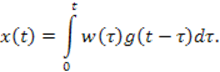
Правая часть последнего выражения есть интеграл свертки, изображение которого, как известно, равно

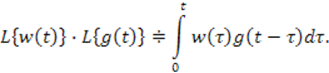
С другой стороны изображение

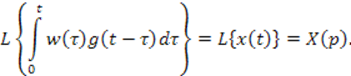
так как есть изображение входного сигнала, получается

Следовательно - передаточная функция системы.

Отсюда вывод:

Передаточная функция системы есть изображение импульсной переходной (весовой) функции этой системы. Это обстоятельство делает возможным найти импульсно переходную функцию для линейных систем с помощью обратного преобразования Лапласа.

Для примера рассмотрим систему, передаточная функция которой имеет вид

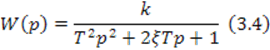
Перепишем последнее выражение

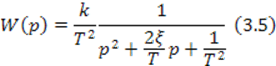
и найдем корни многочлена знаменателя

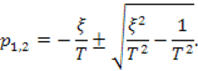
Будем рассматривать случай, когда (в противном случае передаточную функцию можно рассматривать как сумму двух функций со знаменателями в виде многочлена первого порядка).

При этом условии корни многочлена будут комплексные. Обозначим

Тогда выражение (3.5) можно будет представить как

Выражение есть изображение смещенного синуса

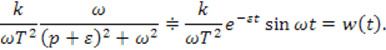
3.4. Передаточные функции соединенных звеньев

Последовательное соединение звеньев

Рассмотрим два последовательно соединенных звена с передаточными функциями и .

Согласно определению, если на вход первого звена подать сигнал , то на выходе будем иметь

, (3.6)

который для второго звена является входным сигналом. Следовательно, на выходе второго звена получим

. (3.7)

Подставим выражение (3.6) в (3.7) получим

Получается, что передаточная функция системы, состоящей из двух последовательно соединенных звеньев, есть произведение передаточных функций этих звеньев.

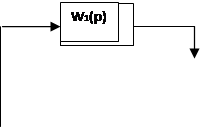
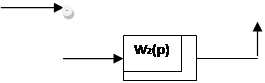
Параллельное соединение звеньев

При параллельном соединении входной сигнал подается сразу на несколько звеньев