Анализ линейных систем автоматического управления: Методическое пособие по дисциплине "Теория автоматического управления", страница 10

или в показательной форме

                        ,

где              -     амплитудная частотная характеристика;

                                                      -   фазовая частотная характеристика,

или в тригонометрической форме

                        .

         Зная вещественную и мнимую части частотной характеристики можно на комплексной плоскости меняя  от 0 до ∞ построить линию. Расстояние от начала координат до точки на этой линии равно амплитудной частотной характеристике , а угол между радиусом – вектором текущей точки и действительной осью есть фазовая частотная характеристика , а сама линия называется годографом.

                   Im

           

                             A(ω)                      

                                                   Re

         Частотная характеристика САУ может быть подтверждена экспериментально. Для подтверждения этого в выражении

                       

сделаем замену переменных:

.

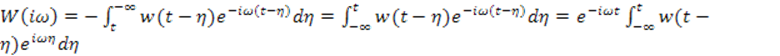         Левую и правую части последнего выражения умножим на

                        .

Комплексную величину  представим в показательной форме, при этом учтем, что

                       

или

                        .

         Воспользуемся формулой Эйлера и перепишем комплексные величины в тригонометрической форме

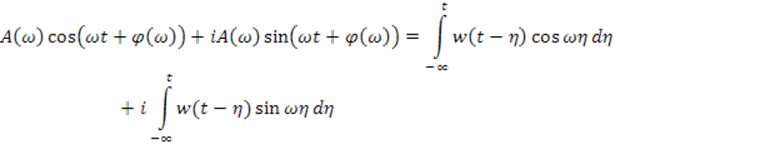
         Известно, что две комплексные величины равны между собой, если равны их действительные и мнимые части. Следовательно

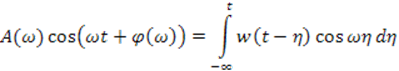
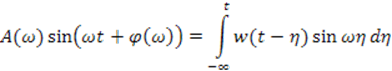
         Полученные выражения есть ни что иное как формулы, определяющие состояние системы при t стремящимся в бесконечность. Входным сигналом, в данных случаях,  косинусоида иди синусоида. На выходе имеет место быть гармонические сигналы с такой же частотой как и на входе, но с амплитудой измененной в  раз и сдвинутой по фазе на величину .

Частотные характеристики можно определить отдельно для амплитуды и отдельно для фазы

                                                 

 

                                                                                                                 ω

 

Логарифмические частотные характеристики

         При анализе САУ широко используется логарифмические амплитудные и фазовые частотные характеристики. Рассмотрим, для примера, некую систему с передаточной функцией

                                           

Заменим

                                   .

         Полученное выражение является комплексной величиной, которую можно записать в показательной форме

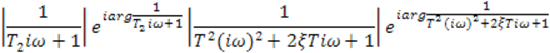
         Соберем в правой части все модули и все экспоненты и прологарифмируем по основанию 10 левую и правую части

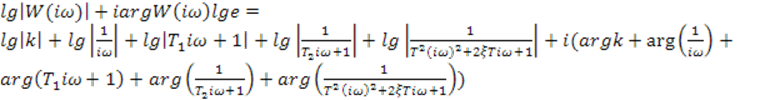(3.8)

Т. к. две комплексные величины равны между собой, если равны их действительные и  мнимые части, то выражение (3.8) можно разделить на два равенства:

;                        (3)

        (3.9)

         Если умножить логарифм амплитудной  характеристики на 20, то получим значение увеличения мощности входного сигнал на выходе системы в децибелах (децибел – безразмерная величина).

                         

-  логарифмическая амплитудная частотная характеристика( ЛАЧХА).

                         

      -   логарифмическая фазовая частотная характеристика (ЛФЧХ).

         Для наглядность логарифмические амплитудные и фазовые частотные характеристика изображаются на графиках. Эти графики строятся отдельно, но один под другим. Причем оси абсцисс имеют одинаковые масштабы. По этим осям откладываются логарифмы частоты в линейном масштабе. По осям ординат в линейном масштабе откладываются  соответственно.

L(ω

 

                                                                                             

 

                0                  1                 2                  3

 

                0                  1                 2                  3