Анализ линейных систем автоматического управления: Методическое пособие по дисциплине "Теория автоматического управления", страница 5

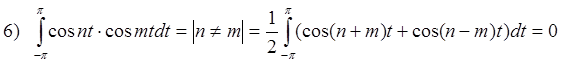
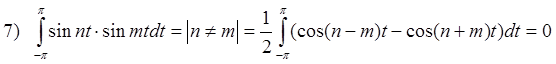
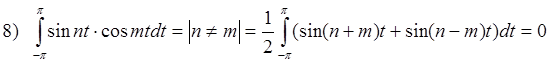
Если система ортогональна, то любую периодическую функцию с периодом T=[a;b] можно представить в виде ряда:

                                                               (2.7)

Определим коэффициенты с_i. Для этого левую и правую части выражения (2.7) умножим на и найдем интеграл от левой и правой частей на интервале ортогональности

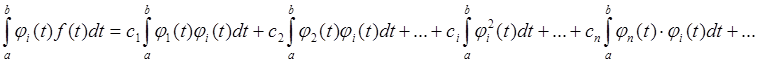                                                                                                                                                          (2.8)

Все интегралы в правой части, кроме 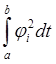  ,будут равны нулю (согласно свойствам ортогональности). В результате получим:

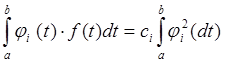
или

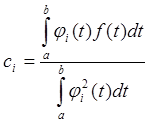                                         (2.9)

Выражение (2.7) называется рядом Фурье в общем виде, а (2.9) – коэффициентом Фурье.

Для тригонометрических систем коэффициенты Фурье определяются.

Для основной системы:

;

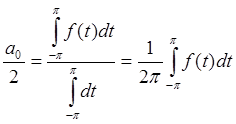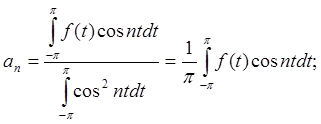                                                                                                                                                                            (2.10)

а сам ряд будет иметь вид

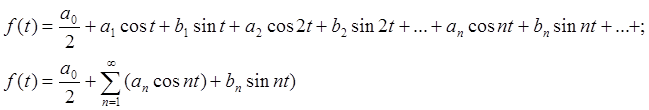                 (2.11 )

Для тригонометрической системы общего вида:

;

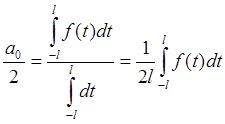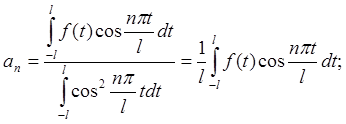                                                                                                                                                                       (2.12)

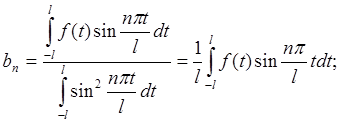
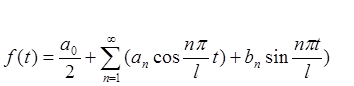                                                                       (2.13)

Коэффициенты (2.10) и(2.12) и ряды (2.11) и (2.13) в некоторых случаях удобней представить в комплексной форме.

В соответствии с формулами Эйлера

 ;  ;

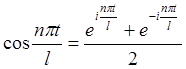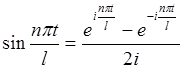Выражение (2.13) можно записать как

.

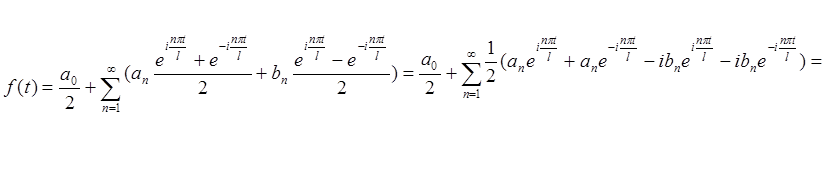
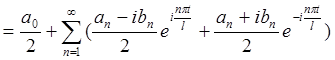Если обозначить                   ,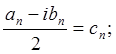

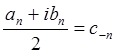то ряд Фурье (2.13) примет вид

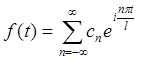                                                                   (2.14).

Это и есть ряд Фурье в комплексной форме.

В комплексную форму можно перевести и коэффициенты Фурье:

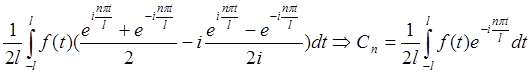
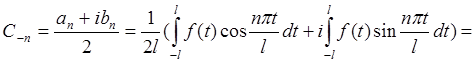
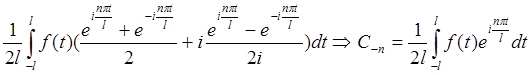
2.3.2.  Интеграл Фурье

Пусть f(t) – гладкая или кусочно - гладкая и абсолютно интегрируемая функция (несобственный интеграл 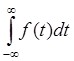- конечная величина).

Представим эту функцию в виде ряда Фурье, использую ортогональную систему общего вида:

.

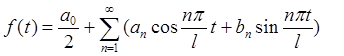Подставим в последнее выражение вместо 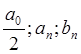их значения

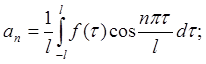
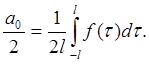
Получим:

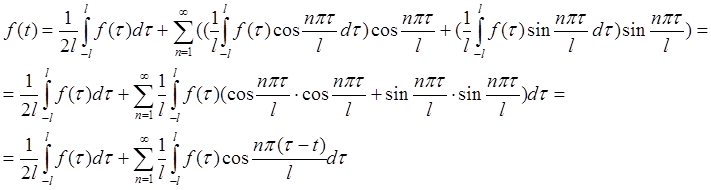
В ряд Фурье можно раскладывать только периодические функции с периодом 2l. Если есть необходимость разложить в ряд непериодическую функцию, то её можно представить как функцию с периодом, стремящимся в бесконечность. То есть надо найти предел ряда Фурье при .

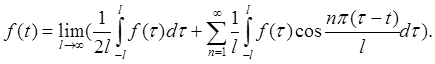
Первое слагаемое  можно исключить (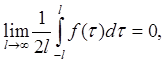так как 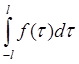- конечная величина по условию)

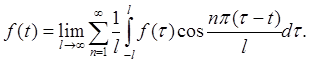
Обозначим 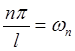            (из физики известно, что 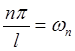- круговая частота ), тогда

                                  

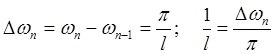
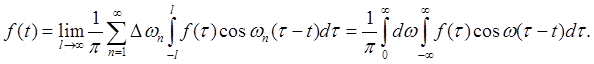
Иногда интеграл Фурье записывают  в другом виде:

 

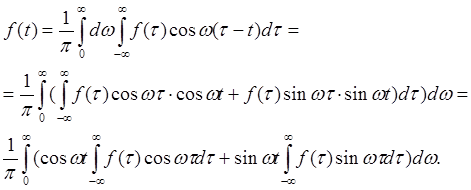
Обозначим :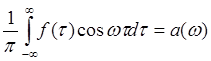             

                                  

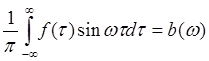
Тогда интеграл Фурье примет вид:

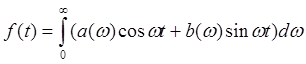
Комплексная форма интеграла Фурье.

Интеграл Фурье как и ряд Фурье можно представить в комплексной форме. Для этого сначала запишем , что

              есть четная функция относительно ω, следовательно

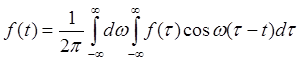
Очевидно, что 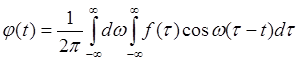 - нечетная функция и на симметричных пределах интегрирования  .

С учетом сделанных замечаний интеграл Фурье можно записать в виде

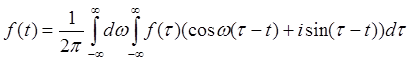
или с учетом формулы Эйлера,

 

Преобразование Фурье.

Формально преобразование Фурье представляет собой сокращение объема записей за счет введения обозначений:

Обозначим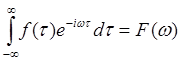 

Последнее выражение называется преобразованием Фурье. Если теперь в интеграл Фурье вместо внутреннего интеграла подставить F(ω), то получим обратное преобразование Фурье.

 

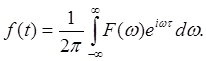
Замечание 1: Преобразование Фурье (как впрочем и другие преобразования) обладает замечательным свойством : каждому значению функции f(t) соответствует вполне определенной и единственное значение F(ω).

Замечание 2.  Преобразование Фурье позволяет перейти от исследования САУ во временной области к исследованию системы в частотной области.

2.4.  Операторные методы исследования САУ

2.4.1.  Преобразования Лапласа