Анализ линейных систем автоматического управления: Методическое пособие по дисциплине "Теория автоматического управления", страница 15

 

                                                  Рис.

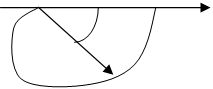
6)  Логарифмические амплитудные и фазовые частотные характеристики колебательного звена удобно строить с помощью асимптот. При значениях   логарифмическая амплитудная характеристика

                         

сколь угодно близко к прямой линии  ,  а при  - к прямой  .

При построении фазовых характеристик низкочастотной асимптотой является ось абсцисс,

а высокочастотной – прямая линия, параллельная оси абсцисс и отстоящая от нее на величину    .                                

               L(ω)

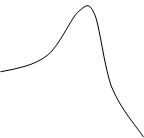
                                                                ξ=0,1                                                                                                   

 

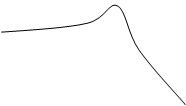                                                                  ξ=0,3

                                                                                                       lgω

                                     ξ=1

        

 

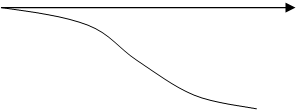                                                                                                 lgω

           -π/2   _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _

                  -π

3.7.  Анализ качества систем автоматического управления

Система автоматического управления должна удовлетворять ряду требований. Количество этих требований может быть довольно большим, но все их можно объединить  в четыре группы:

1) Определение устойчивости и запаса устойчивости САУ;

2) Оценка величины ошибки при различных режимах работы;

3) Оценка быстродействия САУ;

4) Обобщенная (интегральная) оценка работы САУ.

3.7.1. Устойчивость  САУ

Устойчивость является одним из основных показателей работы системы автоматического управления. Дело в том, что работоспособной является только устойчивая система. Но кроме собственно устойчивости надо знать и степень устойчивости системы. Если система находится близко к границе устойчивости, то небольшие изменения параметров системы могут привести к потере устойчивости. Если система очень устойчива, то она становится «ленивой» (плохо управляемой). Получается, что кроме устойчивости необходимо знать запас устойчивости и управляемость системы.

Ответ на вопрос: устойчива система или нет можно искать как во временной области так и в частотной.

Исследование устойчивости во временной области

Построение переходного процесса

Самый очевидный подход к определению устойчивости САУ – это анализ переходного процесса системы после воздействия на нее внешнего возмущения. В соответствии с теоремой Ляпунова А.М. система является устойчивой, если в результате действия малых возмущений она совершает малое отклонение, а при прекращении действия этих возмущений она (система) возвращается к номинальному состоянию.

Математическая модель линейной системы, на которую не действует внешнее возмущение, есть линейное однородное дифференциальное уравнение n – го порядка

                                              . (3.15)

Его решение имеет вид:

                                                                    (3.16)

и оно для устойчивой системы при   должно стремиться к нулю. Это возможно только в том случае, если все слагаемые выражения (3.16) будут стремиться к нулю. А это значит, что все действительные части     должны быть меньше нуля. В этом случае считается, что система обладает асимптотической устойчивостью. Для линейных систем асимптотическая устойчивость является необходимым и достаточным условием устойчивости САУ.

Из приведенных рассуждений следует, что определения устойчивости системы надо:

         - решить уравнение (3.15);

         - построить траекторию изменения выходного состояния системы во времени;

         - произвести анализ полученного переходного процесса.