Анализ линейных систем автоматического управления: Методическое пособие по дисциплине "Теория автоматического управления", страница 21

То есть амплитудно – фазовая характеристика разомкнутой системы будет иметь разрыв второго рода. Для исключения неопределенности заменим корень  на бесконечно малую отрицательную вещественную величину  . Тогда, вместо    получим сомножитель  , модуль которого    при  стремится к нулю, а фаза изменится от нуля при    до    при  .

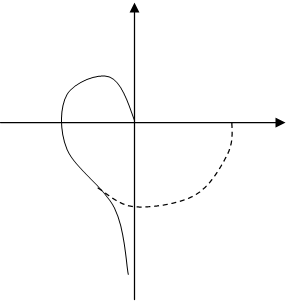
На рисунке сплошной линией показан годограф , а пунктирной - . На высоких частотах эти годографы совпадают. Часть годографа, обозначенного пунктиром, называют дополнением в бесконечность.

 

Аналогично строятся годографы для  При этом дополнение в бесконечность должно проходить   квадрантов.

Если объединить все три случая, то критерий Найквиста можно сформулировать следующим образом:

Для устойчивой замкнутой системы автоматического управления необходимо и достаточно, чтобы разность между числом положительных и отрицательных переходов частотного годографа комплексной передаточной функции разомкнутой системы   через отрицательную действительную полуось от -1 до  была равна    ( – число корней характеристического уравнения разомкнутой системы, лежащих в правой полуплоскости).

 

 

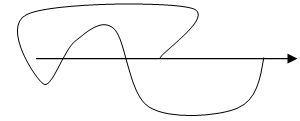Система устойчива в разомкнутом и замкнутом состояниях (годограф не охватывает точку с координатами (-1; i0)).

 

                                                                                                       Система в разомкнутом состоянии

                                                                                                       Неустойчива (, но устойчива в

                                                                                                       замкнутом (годограф имеет два              

                                                                                                                                    положительных и один

                                ˚  -1                                                                отрицательных переход через

                                                                                                       отрицательную часть действительной

                                                                                                       полуоси).

Замечание. Переход считается положительным, если при этом годограф охватывает точку с координатами (-1; i0) против часовой стрелки.

Запас устойчивости

Рассмотрим систему автоматического управления, передаточная функция которой в разомкнутом состоянии имеет вид

                                             .

Перейдем в частотную область. Для этого заменим p на iω  

.

Очевидно, что система будит находиться на границе устойчивости, если годограф будет пересекать действительную ось в точке с координатами . Следовательно

                                              

или

Из последнего выражения определим значение критической частоты

                                              .

На этой частоте действительная часть выражения () должна быть равна -1

                             .

Получается, что

                                              .

Если   , то система устойчива. Чем дальше с правой стороны от критической точки годограф пересекает действительную ось, тем более устойчивой будет система.

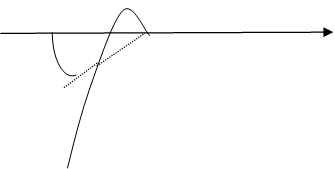
Замечание 1. Запас устойчивости по фазе и амплитуде удобно определять с помощью единичной окружности с центром в начале координат. Если годограф пересекает эту окружность раньше чем он пересекает ось абсцисс в отрицательной полуплоскости, то система устойчивая. Если наоборот – то система неустойчива. Более того угол    (рис. ) определяет запас устойчивости по фазе.

 

Устойчивость системы с помощью критерия Найквиста удобно определять с помощью логарифмических частотных характеристик.

Система будет устойчивой, если логарифмическая амплитудная характеристика пересечет ось абсцисс раньше чем фазовая характеристика пересечет линию, соответствующею фазовому сдвигу равному .