Анализ линейных систем автоматического управления: Методическое пособие по дисциплине "Теория автоматического управления", страница 13

Из выражений (3.11) и (3.12) следует, при изменении частоты    амплитуда меняется от  до 0, а фазовый сдвиг остается неизменным и равным

                        Im

                                               Re

                                  

6) Логарифмические амплитудные и фазовые частотные характеристики идеального интегрирующего звена

                         

Идеальное интегрирующее звено имеет логарифмическую амплитудную частотную характеристику в виде прямой линии с наклоном в 20дб/дек в сторону уменьшения. Фазовая характеристика на всех частотах остается постоянной величиной равной –.

3.6.4.  Апериодическое звено

Примером апериодических звеньев могут служить многие двигатели (электрические, гидравлические, пневматические и т.д.), электрические генераторы постоянного тока, RC- и LC-цепи …

1)  Передаточная функция апериодического звена

                         

2)  Математическая модель апериодического звена

                         

3)  Переходной процесс апериодического звена

Определим переходный процесс апериодического звена при воздействии на него единичного входного сигнала. Для этого решим линейное дифференциальное уравнение первого порядка

                                     .               (3.13)

Воспользуемся методом Бернулли, согласно которому неизвестную функцию представим произведением    ,  тогда   и уравнение запишется в виде

                                     

или

                                     .

Выберем   таким образом, чтобы

                                                                .

Значение    обращает   в ноль, уравнение () приводится к виду

                                     .

Разделив переменные и проинтегрировав левую и правую части, определим    u

                                     .

Теперь можно записать общее решение уравнения (3.13)

Если в момент времени t=0   , то    и решение уравнения (3.13) примет вид

                                                .

Если , тогда характер изменения состояния системы можно определить выражением

                                     

          x(t)

                                  

                _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _

                                      

 

                                      tпп                                        t        

Переходный процесс, при  , сколь угодно близко приближается к значения  , но никогда его не достигая. На практике принято считать, что переходный процесс апериодического звена, завершен, если он отличается от номинального значения не более чем на 5%. Момент попадания в пятипроцентный коридор (tпп) принято считать временем переходного процесса. Найдем tпп.  Для этого воспользуемся выражением (3.13)

                                    

или

                                     .

Прологарифмируем последнее выражение

                                    .

Следовательно   . Получается, что постоянная времени Т характеризует быстродействие системы.

4)  Импульсная переходная функция апериодического звена.

Так как передаточная функция есть изображение по Лапласу импульсной переходной функции, то

                        .

5)  Амплитудно – фазовая частотная характеристика апериодического звена. Для ее определения заменим в передаточной функции  p  на iω  

                        .

Определим амплитуду как модуль комплексной величины ()

                        

и фазу как аргумент комплексной величины ()

                         

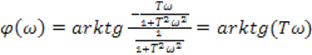
        Im

k

                                      Re

 

                           

При изменении частоты от 0 до  амплитуда  меняет свое значение от k до 0, а фазовый сдвиг меняется от 0 до .

6)  Логарифмические амплитудные и фазовые частотны характеристики апериодического звена. Амплитудную характеристику можно построить с помощью выражения

             .