2. Составить
определитель Гурвица. Для этого по главной диагонали (с левого верхнего угла в
правый нижний угол) начиная с коэффициента ![]() по порядку расположить коэффициенты
уравнения (). После этого заполнить столбцы определителя начиная от соответствующего
элемента главной диагонали. При движении вверх - располагаются коэффициенты с
возрастающим индексом, а при движении вниз – коэффициенты с убывающим индексом.
Если на каком-то месте должен стоять коэффициент, у которого индекс больше n или меньше нуля, то на это
место записывается ноль
по порядку расположить коэффициенты
уравнения (). После этого заполнить столбцы определителя начиная от соответствующего
элемента главной диагонали. При движении вверх - располагаются коэффициенты с
возрастающим индексом, а при движении вниз – коэффициенты с убывающим индексом.
Если на каком-то месте должен стоять коэффициент, у которого индекс больше n или меньше нуля, то на это
место записывается ноль
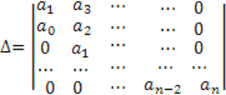 .
.
3. Определяются все диагональные миноры:
![]() ;
;
![]() ;
;
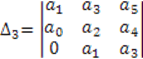 ;
;
![]()
![]() .
.
Система будет устойчивой, если все диагональные миноры будут строго больше нуля.
Замечание
1. Определитель ![]() можно не вычислять, так как его знак
будет совпадать со знаком определителя
можно не вычислять, так как его знак
будет совпадать со знаком определителя ![]() , если
, если ![]() будет больше нуля.
будет больше нуля.
Замечание 2. Система будет устойчива тогда и только тогда, если все коэффициенты уравнения (3.19) будут больше нуля (необходимое, но не достаточное условие устойчивости).
Для того чтобы убедиться в справедливости последнего утверждения рассмотрим несколько примеров.
Пусть n=1, тогда уравнение () примет вид:
![]() . (3.20)
. (3.20)
Коэффициент ![]() (по условию)
(по условию)
![]() .
.
Следовательно, все коэффициенты (.) для устойчивой системы должны быть больше нуля (условие необходимое и достаточное).
Пусть n=2, тогда уравнение () будет иметь вид:
![]() . (3.21)
. (3.21)
Определитель Гурвица, в этом случае, запишется как
![]() .
.
По критерию
система будет устойчива, если ![]() и
и ![]() . Получается, что система будет устойчивой,
если все коэффициенты уравнения (..) будут больше нуля. Это условие, как и в
предыдущем случае, является необходимым и достаточным.
. Получается, что система будет устойчивой,
если все коэффициенты уравнения (..) будут больше нуля. Это условие, как и в
предыдущем случае, является необходимым и достаточным.
Пусть n=3, тогда уравнение () примет вид:
![]() , (3.22)
, (3.22)
а определитель Гурвица можно представить следующим образом:
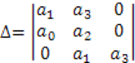 .
.
Все диагональные миноры, если система устойчива, должны быть больше нуля.
![]() (3.23)
(3.23)
![]() , (2.24)
, (2.24)
![]() . (3.25)
. (3.25)
Из условия
критерия Гурвица ![]() , из (3.23)
, из (3.23) ![]() , из (3.25)
, из (3.25) ![]() и как следствие,
и как следствие, ![]() . Получается, что все коэффициенты
уравнения (3.22) должны быть положительными. Это условие является необходимым,
но не достаточным, так как они должны находиться в таком соотношении, чтобы
выполнялось условие (3.24).
. Получается, что все коэффициенты
уравнения (3.22) должны быть положительными. Это условие является необходимым,
но не достаточным, так как они должны находиться в таком соотношении, чтобы
выполнялось условие (3.24).
Если продолжить рассмотрение систем более высокого порядка, то можно прийти к выводу, что положительность коэффициентов уравнения (3.19) является необходимым условием устойчивости системы. Для выполнения достаточного условия необходимо, чтобы были положительными все диагональные миноры определителя Гурвица.
Критерий Гурвица удобно использовать для систем низкого порядка. При исследовании систем высокого порядка: во первых - резко возрастает объем вычислений; во вторых – в случае неустойчивости системы нет возможности с помощью критерия определить как надо изменить параметры системы, чтобы она стала устойчивой.
Критерий устойчивости Михайлова
Михайлов предложил исследовать систему на устойчивость с помощью годографа, построенного для системы, на которую не действуют никакие внешние силы. Математическая модель такой системы представляет собой линейное однородное дифференциальное уравнение
![]() ,
,
характеристическое уравнение,
которого есть знаменатель передаточной функции системы
![]() .
.
Разложим многочлен знаменателя на элементарные сомножители
![]() ,
,
где ![]() - корни многочлена (I
= 1, 2, … ,n).
- корни многочлена (I
= 1, 2, … ,n).
Перейдем в
частотную область. Для этого заменим p на ![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.