3) Переходной процесс. а)Если входной
сигнал есть функция ![]() , то на выходе будет дельта – функция δ(t). б)Если входное
воздействие есть функция
, то на выходе будет дельта – функция δ(t). б)Если входное
воздействие есть функция ![]() , то на выходе будет постоянная величина, равная
, то на выходе будет постоянная величина, равная
![]()
![]() x(t)
x(t)
![]()
![]() k б)
k б)
![]() а)
а)
![]() t
t
Рис.
4) Импульсная переходная функция
![]()
5) Амплитудно – фазовая частотная характеристика. Для ее определении в передаточной функции заменим p на iω
![]()
Амплитудная характеристика будет равна
![]() .
.
Фазовая характеристика
![]()
6) Логарифмические амплитудная и фазовая частотные характеристики
![]()
Так как при
построении графика ЛАЧХ по оси абсцисс откладывается ![]() в линейном масштабе, график логарифмической амплитудной
частотной характеристики идеального дифференцирующего звена есть прямая линия и
для ее построения достаточно знать две точки. Эти точки удобно определять при
частоте
в линейном масштабе, график логарифмической амплитудной
частотной характеристики идеального дифференцирующего звена есть прямая линия и
для ее построения достаточно знать две точки. Эти точки удобно определять при
частоте ![]() , тогда
, тогда
![]()
и при частоте ![]() ,
тогда
,
тогда
![]()
График ЛАЧХ идеального дифференцирующего звена можно построить иначе. Дело в том, наклон его не зависит ни от частоты, ни от коэффициента усиления и всегда обеспечивает рост амплитудной характеристика при увеличении частоты в 10 раз (на декаду) на 20дб. Действительно, если увеличить частоту в 10 раз, то характеристика получит приращение
![]()
Таким образом для построения логарифмической амплитудной частотной характеристики достаточно иметь только одну точку, через которую надо провести прямую с наклоном 20 дб на декаду.
Фазовая характеристика идеального дифференцирующего звена
L(ω)
![]()
![]()
 |
![]()
![]()
![]()
![]()
![]()
![]()
0 1 2 3
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 0 1
2 3
0 1
2 3 ![]()
3.6.3. Идеальное интегрирующее звено
Примером интегрирующего звена может служить электронное устройство, собранное на базе операционного усилителя
![]()
![]() C
C
![]()
![]()
![]()
![]()

R
![]()
![]()
![]()
![]()
![]()
Uвх Uвых=x(t)
Рис.
Или гидравлический
демпфер, у которого скорость движения пропорциональна приложенной силе ![]() . Следовательно перемещение
. Следовательно перемещение
![]() ,
,
где F - сила, действующая на поршень (входная величина);
S - коэффициент вязкого трения.
1) Передаточная функция идеального интегрирующего звена
![]()
2) Математическая модель идеального интегрирующего звена
![]() (3.10)
(3.10)
3) Переходной процесс идеального
интегрирующего звена. Для его определения подадим на вход ![]() и решим дифференциальное уравнение ()
и решим дифференциальное уравнение ()
![]()
![]()
![]()
Если при ![]()
![]() , то
, то ![]() . Следовательно, график переходного процесса идеального
интегрирующего звена будет представлять из себя прямую линию с угловым
коэффициентом равным к и проходящей через точку с координатами (0;
х0)
. Следовательно, график переходного процесса идеального
интегрирующего звена будет представлять из себя прямую линию с угловым
коэффициентом равным к и проходящей через точку с координатами (0;
х0)
![]() x(t)
x(t)
 |
x0
![]() t
t
4) Импульсная переходная функция. Для ее определения найдем оригинал передаточной функции идеального интегрирующего звена
![]()
5) Амплитудно – фазовая частотная характеристика идеального интегрирующего звена.
![]()
![]() (3.11)
(3.11)
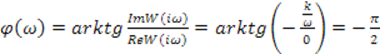 (3.12)
(3.12)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.