Анализ линейных систем автоматического управления: Методическое пособие по дисциплине "Теория автоматического управления", страница 20

                               .                  (3.26)

С одной стороны каждый из сомножителей есть комплексная величина

Аргумент комплексного числа    будет равен

                                .

С другой стороны каждый из сомножителей (3.26) можно представить вектором на комплексной плоскости, начало которого находится в точке  , а конец, при изменении частоты от минус бесконечности до плюс бесконечности, скользит по мнимой оси. При этом, если  находится в левой полуплоскости, то поворот вектора составит угол  (против часовой стрелки), если   находится в правой  полуплоскости, то поворот вектора будет равен    (по часовой стрелке). Следовательно, угол охвата начала координат комплексной плоскости годографом функции , если все корни характеристического уравнения лежат в левой полуплоскости, составит . Если  корней находятся в правой полуплоскости, то угол охвата будет равен . Система будет устойчивой, если все корни будут находиться в левой полуплоскости. Это условие является необходимым и достаточным.

Критерий Найквиста

Одним из самых распространенных критериев устойчивости линейных систем является критерий Найквиста. Он позволяет определить устойчивость замкнутой системы по характеристикам разомкнутой системы. Кроме того с его помощью можно оценить запас устойчивости системы. Критерий Найквиста – это графоаналитический частотный критерий.

Предположим, что передаточная функция разомкнутой системы есть правильная рациональная дробь (в большинстве практических случаях это так и есть)

                                                            ,

где      - ;

            -  .

Если эта система охвачена жесткой обратной связью, то передаточная функция замкнутой системы будет иметь вид

                                                              .

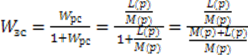Так как дробь    правильная, то многочлены    и   имеют одинаковые порядки. Но многочлен     есть характеристическое уравнение замкнутой системы, а многочлен     - характеристическое уравнение разомкнутой системы.

Рассмотрим  три случая:

1. Система в разомкнутом состоянии устойчива. Тогда, согласно критерию Михайлова, при изменении частоты от нуля до бесконечности аргумент должен быть равен

Для того, чтобы и замкнутая система была устойчивой необходимо, чтобы

Но тогда

Получается, что годограф, построенный для    не должен охватывать точку на комплексной плоскости с координатами  . Но так как   отличается от  на 1, то условие устойчивости можно получить непосредственно для характеристики  .  В этом случае годограф не должен охватить точку с координатами .

Таким образом для того чтобы замкнутая система была устойчивой при устойчивой разомкнутой системе необходимо и достаточно, чтобы частотный  годограф комплексной передаточной функции  при изменении частоты от нуля до бесконечности не охватывал точку с координатами .

2. Система в разомкнутом состоянии неустойчива. Если это так, то корней характеристического полинома М(р) будет лежать в правой полуплоскости и аргумент этого полинома при изменении частоты от нуля до бесконечности совершит поворот на угол

                                              .

Если замкнутая система будет при этом устойчивой, то

                                             ,

а аргумент функции  будет равен

                .

Получается: система будет устойчивой, если частотный годограф комплексной передаточной функции разомкнутой системы охватит     раз в положительном направлении точку с координатами  .

Замечание. Предыдущее определение есть частный случай последней формулировки.

3. Система в разомкнутом состоянии находится на границе устойчивости. Это возможно, если знаменатель передаточной функции разомкнутой системы имеет корни равные нулю

                                                              ,

где         – число нулевых корней.  Рассмотрим случай, когда  . При  

а аргумент

                                                             .