![]() – весовые коэффициенты внешних воздействий.
– весовые коэффициенты внешних воздействий.
Применим к выражению (3.1) преобразование Лапласа. При этом будем считать, что
![]() – изображение неизвестной функции (состояния системы)
– изображение неизвестной функции (состояния системы)
![]() – изображение входного воздействия.
– изображение входного воздействия.
Кроме того будем считать , что все
значения ![]() равны нулю.
равны нулю.
![]()
Полученное в образах
преобразования Лапласа уравнение является алгебраическим и оно легко
разрешается относительно ![]()

Получается, что для определения изображения состояния системы надо изображение входного сигнала умножить на коэффициент
![]() (3.2)
(3.2)
Этот коэффициент называется передаточной функцией.
Выражение (3.2) чаще всего является рациональной дробью, в числителе в знаменателе которой находятся многочлены. Эти многочлены, на основании основной теоремы алгебры, можно представить через элементарные сомножители
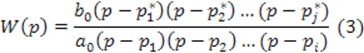
Где ![]() - корни много членов знаменателя и числителя соответственно.
- корни много членов знаменателя и числителя соответственно.
Корни многочленов могут быть:
- равными нулю;
- действительными (не равными нулю);
- комплексными.
Все сомножители (3) можно разделить на 7 групп, каждая из которых включает в себя определенный вид определенной функции.
1.
![]() – усилительное звено;
– усилительное звено;
2.
![]() – идеальное дифференцирующее звено;
– идеальное дифференцирующее звено;
3.
![]() – идеальное интегрирующее звено;
– идеальное интегрирующее звено;
4.
![]() – форсирующее звено 1-го порядка;
– форсирующее звено 1-го порядка;
5.
![]() - апериодическое звено;
- апериодическое звено;
6.
![]() - форсирующее звено 2-го порядка (корни многочлена числителя –
комплексные);
- форсирующее звено 2-го порядка (корни многочлена числителя –
комплексные);
7.
![]() - колебательное звено (корни многочлена знаменателя –
комплексные).
- колебательное звено (корни многочлена знаменателя –
комплексные).
Замечание
Перечисленные звенья получены в результате формального математического преобразования и не всегда совпадают с реальными (физическими) устройствами. Более того, идеальные звенья физически воспроизвести нельзя.
3.2. Типовые входные сигналы
При исследовании САУ на вход системы целесообразно подавать вполне определенные сигналы. Для этого используют пять видов сигналов.
1. Единичный входной сигнал
![]()
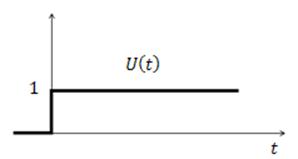
Преобразование Лапласа:
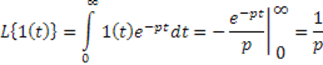
Рис.
2. Линейно нарастающий входной сигнал.
![]()
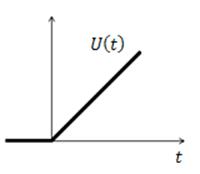
Преобразование Лапласа:
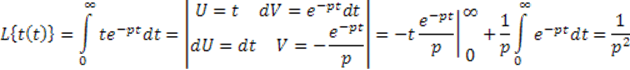
Рис.
3. Гармонические входные сигналы.
![]()
Преобразование Лапласа:
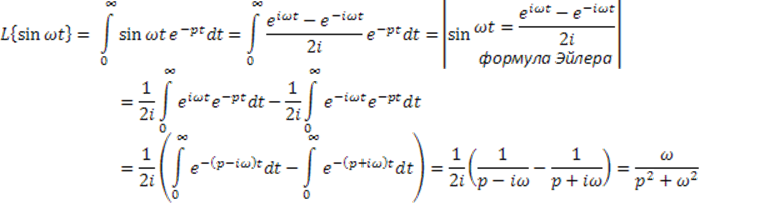
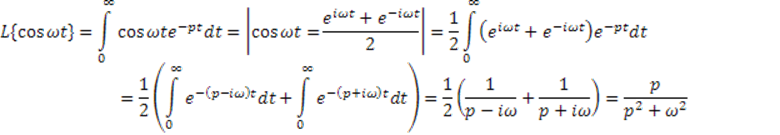
4. Экспоненциальный входной сигнал
![]()
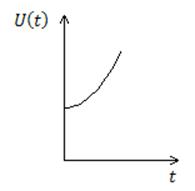 Преобразование Лапласа:
Преобразование Лапласа:
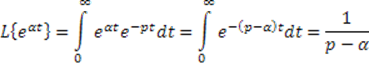
Рис.
5. Дельта-функция Дирака
Функция
![]()
При условии, что
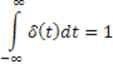
Физически воспроизвести такую функцию нельзя. Да и с позиции классической математики δ - функция не является функцией в обычном смысле. Однако в классе обобщенных функций δ - функция имеет право на существование.
Смещенная δ -
функция ![]() определяется равенством
определяется равенством
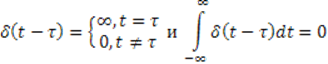
Дельта - функцию можно считать
производной от функции ![]()
![]()
Изображение по Лапласу:
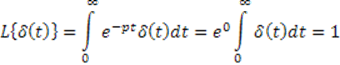
У δ-функции есть очень важное свойство:
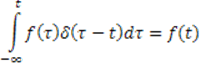
Функция ![]() . Во всех
остальных точках она (эта функция) будет умножаться на ноль. Следовательно
. Во всех
остальных точках она (эта функция) будет умножаться на ноль. Следовательно ![]() будет значимой
только в точке
будет значимой
только в точке ![]() и не изменится.
То есть она окажется постоянной и ее можно вынести за знак интеграла:
и не изменится.
То есть она окажется постоянной и ее можно вынести за знак интеграла:
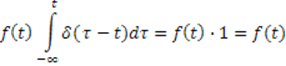
Есть несколько способов моделирования δ - функции. Рассмотрим два из них.
1.
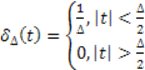
Очевидно, что при ![]() ,
, ![]() и
и
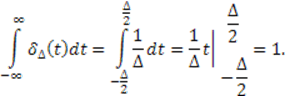
Так как δ-функция абсолютно интегрируема, то для нее можно выполнить преобразование Фурье
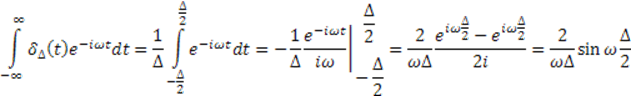
Подставив полученное выражение в обратное преобразование Фурье, получим интеграл Фурье для импульсной функции:
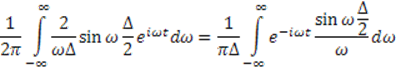
2.
![]()
При ![]() при любом
значении
при любом
значении ![]() .
.
При ![]()
![]()
Выполняется и второе условие δ - функции.
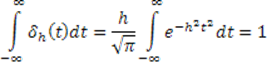
Для того, чтобы убедиться в этом рассмотрим двойной интеграл
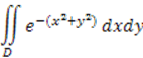
Будем искать этот интеграл для трех областей ![]() .
.
![]() - круг с
радиусом
- круг с
радиусом ![]() , вписанный в
квадрат;
, вписанный в
квадрат;
![]() - квадрат,
в который вписан круг с радиусом
- квадрат,
в который вписан круг с радиусом ![]() ;
;
![]() – круг с
радиусом
– круг с
радиусом ![]() , в который
вписан квадрат области
, в который
вписан квадрат области ![]() .
.
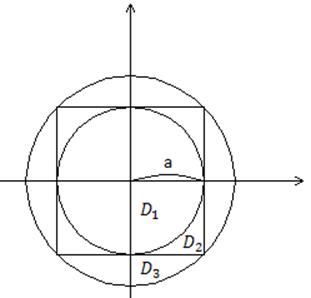 Для определения интеграла по области
Для определения интеграла по области ![]() перейдем в
полярную систему координат.
перейдем в
полярную систему координат.
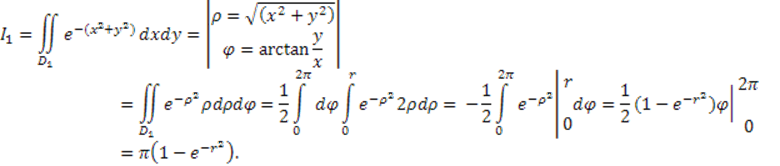
Аналогично
берем интеграл по области ![]()
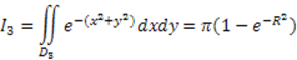
Найдем
интеграл по области ![]()
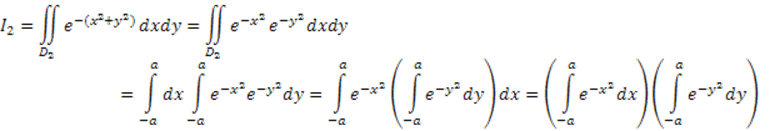
Значение определенного интеграла от обозначения переменной не зависит. Следовательно в последнем выражении значения в скобках одинаковы. А раз так, то
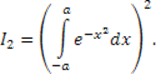
Обратим внимание на тот факт, что неравенство
![]()
Будет выполняться при всех значениях параметров областей. В
том числе и при ![]() (как следствие
(как следствие ![]() ).
).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.