Полученное аналитическое выражение решения уравнения (2.3) позволяет ответить на многие вопросы по работе системы, которая описана данным уравнением:
- как будет выглядеть переходный процесс;
- будет ли система устойчива или нет;
- каково быстродействие системы;
- какова точность системы.
Исследование САУ, поведение которой описывается линейными дифференциальными уравнениями высших порядков, путем аналитического решения этих уравнений – задача не из простых. Но если порядок уравнения не очень высокий (например, второй), коэффициенты уравнения не меняются во времени, а внешнее воздействие может быть описано математическим выражением вида:
![]() ,
,
где Pm(t) и Qm(t) - многочлены порядка m и n соответственно,
то общее решение уравнения
![]() (2.6)
(2.6)
можно найти в виде
![]() ,
,
где
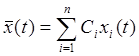 - общее решение
соответствующего однородного уравнения,
- общее решение
соответствующего однородного уравнения,
![]() - частные решения,
образующие фундаментальную группу решений соответствующего однородного
уравнения,
- частные решения,
образующие фундаментальную группу решений соответствующего однородного
уравнения,
x*(t) - какое-либо частное решение
неоднородного уравнения
Частные решения для фундаментальной группы соответствующего однородного уравнения можно определить с помощью метода, предложенного Эйлером. Для этого составляется характеристическое уравнение
![]() ,
,
решение которого дает n значений λ. Если решения
- действительные и разные, то ![]() ,
,
- действительные, но имеют кратность
k, то ![]() (i принимает значения от 1 до k),
(i принимает значения от 1 до k),
- комплексные сопряженные, то ![]() и
и ![]() .
.
Частное решение неоднородного уравнения ищется в форме
![]() ,
,
в которой l = max(m,n), Rl(t), Tl(t) –
многочлены порядка l с неопределенными коэффициентами.
Показатель степени s определяется следующим образом:
s = 0,
если число (α + jω) не совпадают ни с одним из корней
характеристического уравнения;
s = k, если число (α + jω) совпадает с корнями
характеристического уравнения кратности k.
На
пример если на систему, собственное поведение которой описывается
дифференциальным уравнением второго порядка, а внешнее воздействие определено
функцией ![]() при начальных условиях
при начальных условиях ![]()
![]() ,
, ![]() .
.
![]()
Требуется найти свободное
(собственное) и вынужденное движение системы.
1) Запишем характеристическое уравнение
![]() ,
,
которое
имеет два решения ![]() ,
, ![]() .
.
Общее
решение однородного уравнения в этом случае будет иметь вид:
![]() .
.
Из начальных условий
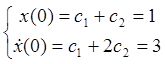
имеем ![]() ,
,
![]() .
.
При этом общее решение однородного уравнения будет иметь вид:
![]()
Для определения общего решения неоднородного уравнения (вынужденного движения системы) зададим частное решение неоднородного уравнения в виде:
![]() . Тогда
. Тогда ![]() , а
, а ![]() .
.
Подставив последние значения в исходное уравнение, получим
![]() .
.
Отсюда
А=1, ![]()
Теперь можно записать общее решение неоднородного уравнения:
![]() .
.
Если заданы начальные
условия, например ![]() ;
; ![]() , то можно
определить произвольные постоянные
, то можно
определить произвольные постоянные
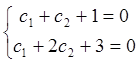
![]()
![]() .
.
Вынужденное движение в этом случае будет:
![]()
2.3. Исследование систем в частотной области
2.3.1. Ряды Фурье
Функция f(t) называется периодической, если f(t)=f(t + πT) ,
Где n=0;±1;±2;±3;…;
T – период.
Любую периодическую функцию можно выразить с помощью системы функций:
φ1 (t); φ2(t);……; φn (t);.., если эта система ортогональна на отрезке длиною T.
Система будет ортогональной на отрезке [a;b], если выполняется следующее условия:
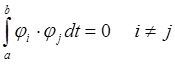
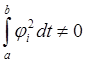
В теории автоматического управления, в основном, используется
тригонометрическая система общего вида: 1; 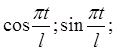
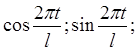 …;
…;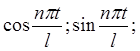 …, которая ортогональная на отрезке [-l; l] или на любом другом отрезке длиной 2l. Или ее частный случай – основная
тригонометрическая система: 1; cos t; sin t; cos 2t; sin 2t;….;cos nt; sin nt;…, которая ортогональная на отрезке
[-π;π] или на любом другом отрезке длиной 2π.
…, которая ортогональная на отрезке [-l; l] или на любом другом отрезке длиной 2l. Или ее частный случай – основная
тригонометрическая система: 1; cos t; sin t; cos 2t; sin 2t;….;cos nt; sin nt;…, которая ортогональная на отрезке
[-π;π] или на любом другом отрезке длиной 2π.
Для того чтобы убедиться в том, что системы ортогональны, найдем 8 интегралов (сделаем это для основной тригонометрической системы):
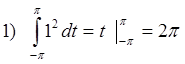
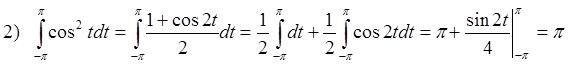
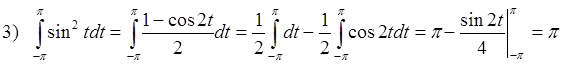
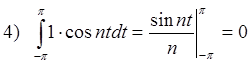
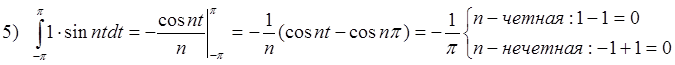
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.