Анализ линейных систем автоматического управления: Методическое пособие по дисциплине "Теория автоматического управления", страница 2

Если координаты вектора состояния измеряются (контролируются), то они называются наблюдаемые, если координаты вектора участвуют в управлении ОУ, то они являются управляемыми (Y={y₁, y₂. …,y_m}^т).

Внешние воздействия можно разделить на:
 -  управление                       U = {u₁, u₂,…,ur}^т;
 -  возмущения.

 Последние могут быть:
-  нагрузкой               G = {g₁, g₂, …, g_s}^т;
-  помехой                 F = {f₁, f₂, ..., f_p}^т

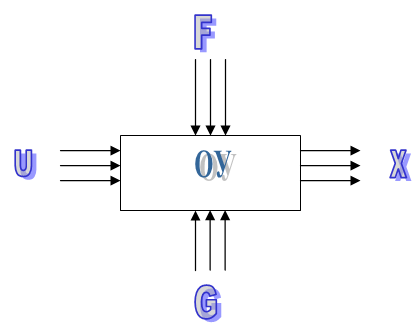
Задача системы управления – поддержание задаваемого режима функционирования объекта управления или другими словами – обеспечить требуемое поведение выходных величин.

Устройства, вырабатывающие управляющее воздействие, называют регулятором (УУ). Оно включает в себя:

-  измерители (датчики времени, температуры, давления, положения объекта в пространстве);
-  преобразователи (устройства, преобразующие один вид сигнала в другой);
-  вычислительные устройства (устройства, формирующие закон управления); 
-         исполнительные механизмы.

Исследование САУ можно проводить теоретически или экспериментально. В данном курсе речь будет идти только о теоретических возможностях исследования системы. Такай принцип оправдан:
                 во первых –                     названием  самого курса («Теория автоматического управления»);
                  во вторых –                    позволяет получить ответы на многие вопросы априорно;
                  в третьих  –                     теория  позволяет не только исследовать САУ, но и создавать новые системы, обладающими нужными качествами.

Для проведения теоретических исследований необходимо иметь математическую модель системы.

Математическое описание объекта позволяет установить связь между входными воздействиями и вектором состояния системы.

Если рассматривается статическое состояние системы (когда все входные воздействия не меняются во времени, а сама система закончила все переходные процессы), то поведение системы описывается алгебраическими уравнениями

F(x, g, f, u) = 0.

Эта математическая модель не позволяет описать поведение системы в динамики, т.к. ступенчатое изменение входного сигнала приводит, согласно этой модели, к ступенчатому изменению выходных параметров, что не соответствует действительности (отсутствует переходный процесс).

Более точно поведение системы описывает дифференциальное уравнение, которое, в случае воздействия на систему только управления, в общем виде, можно представить как

F(x, x’, x’’, …, x⁽ⁿ⁾, u, u’, u’’,…, u^(m), t) = 0.

Это, как правило, нелинейное, нестационарное, неоднородное  дифференциальное уравнение n – го порядка или система нескольких  уравнений.

Создание математической модели САУ

Для определения  математического описания поведения динамики объекта можно воспользоваться двумя подходами:

1)  Использовать законы природы (механики, электротехники, гидравлики и т. д.) Такой способ математического описания можно реализовать, если объект достаточно простой и хорошо изучен.

2)  Использовать опыт разработчиков (эвристический способ). Объект описывается по основным чертам внешнего поведения, без глубокого проникновения в сущность его функционирования. С такой моделью  должны быть проведены: исследования на

адекватность (т.е. насколько модель соответствует поведению реального объекта) и определены границы этой адекватности.

При создании математической модели САУ целесообразно придерживаться следующего алгоритма:

1)  Представить САУ в виде набора отдельных, достаточно простых звеньев;

2)  Составить дифференциальное уравнение для каждого отдельно взятого звена;

3)  Определить уравнения связи;

4)  Составить структурную схему.

2.1.1.  Линейные системы управления

В результате моделирования динамические  процессы системы описываются, как правило, нелинейными, нестационарными, неоднородными дифференциальными уравнениями n – го порядка

F(x, x’, x’’, … , x⁽ⁿ⁾, t) = φ(g, g’, … ,g^(m), t),                             (2.1)

Где      х                      - вектор состояния системы;
            g                     - вектор внешнего воздействия.