Анализ линейных систем автоматического управления: Методическое пособие по дисциплине "Теория автоматического управления", страница 14

Изменяя значение частоты от  0 до   можно построить логарифмическую амплитудную частотную характеристику. Но это же можно сделать много проще, если учесть тот факт, что при  стремлении частоты   амплитуда  , а при стремлении  частоты  амплитудная характеристика стремится к ЛАЧХ идеального интегрирующего звена

                                    .

Получается, что     есть низкочастотная асимптота апериодического звена, а    – высокочастотная асимптота апериодического звена. Нетрудно видеть, что эти асимптоты пересекаются при частоте  . Очевидно, что при этой частоте будет иметь месть максимальная разница между асимптотами и реальной логарифмической амплитудной частотной характеристикой апериодического звена.

                        .

С помощь асимптот удобно строить и фазовую характеристику. При малых частотах асимптотой является ось абсцисс, а при больших – прямая линия, параллельная оси абсцисс и отстоящая от нее на величину равную . Можно заметить, что при частоте    сдвиг по фазе составляет угол .

Анализ ЛАЧХ и ЛФЧХ дает основание считать, что диапазон частот от 0 до  есть полоса пропускания апериодического звена, так как на всем диапазоне  этих частот практически не меняется. На более высоких частотах амплитуда уменьшается с увеличением частоты.

3.6.5.  Колебательное звено

Примером колебательного звена может служить RLC – цепь или амортизатор автомобиля.

1)  Передаточная функция колебательного звена

                                     .

2)  Математическая модель колебательного звена имеет вид

                                    .

3)  Переходной процесс колебательного звена определим, решив линейное, стационарное дифференциальное уравнение второго порядка, подав на его вход единичный входной сигнал

                                    .            (3.14)

Общее решение уравнения ()определим в виде суммы

                                    ,

где    – общее решение соответствующего  однородного дифференциального уравнения,

                          - какое-либо частное решение неоднородного уравнения.

Для определения общего решения однородного уравнения решим характеристическое уравнение

                                     

                                     .

Звено можно отнести к колебательному, если . В этом случае корни характеристического уравнения будут комплексными. Обозначим , тогда

                                     .

Пусть  . В этом случае общее решение соответствующего однородного уравнения можно представить как

Для определения общего решения неоднородного уравнения воспользуемся методом подбора. Так как правая часть исходного уравнения есть многочлен нулевого порядка, будем частное решение в виде , тогда , . Следовательно

                                                                     .

В результате общее решение уравнения (3.14) примет вид

                                    

            x(t)

           

            k _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _

 

                                   Рис.                                   t

4) Импульсная переходная функция колебательного звена может быть определена с помощью обратного преобразования Лапласа передаточной функции

                                    .

Знаменатель последнего выражения есть характеристическое уравнение (3.14), корни которого равны

                                     .

Следовательно передаточную функцию колебательного звена можно представить как

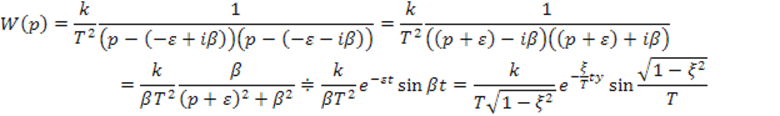
5) Амплитудно - фазовая частотная характеристика колебательного звена определяется путем замены в передаточной функции  p на iω и выделения в полученной комплексной величине модуля и аргумента.

            ;

                                    ;

                                    ;

             ;

                                       .

При изменении ω от нуля до бесконечность     меняется от  k до нуля,  - от нуля до .

                        Im

                                                   k          Re