Вывод: В данной работе была использована аппроксимация переходной характеристики объекта с передаточной функцией пятого порядка с запаздывающим аргументом методом последовательного аппроксимирования. Данный метод аппроксимации не подходит для построения экспериментальной переходной характеристики, так как ошибка аппроксимации составила ∆= 6,857 %, что выше допустимого в инженерных расчетах значения ∆= 5 %.
3. Выбор регулятора.
3.1. Выбор типа регулятора.
Под выбором типа регулятора подразумевается выбор простейшего закона регулирования, наиболее дешевого и простого в эксплуатации регулятора, обеспечивающего при различных возмущениях в заданных пределах динамическую ошибку, время регулирования и статическую ошибку. Следовательно, тип регулятора любой автоматической системы может быть определен либо по трем из этих показателей, либо по некоторым из них. Поэтому в соответствие с требованиями технологии в качестве заданного выбирают один из типовых переходных процессов.
Ориентировочно характер
действия регулятора определяют по величине соотношения: 
.
а) если < 0.2 – позиционный регулятор.
б) если 0,2 ≤≤ 1 – регулятор непрерывного действия.
в) если > 1 – многоконтурная система
управления.
По технологическим условиям уровень конденсата в конденсатотводчике не должен превышать 80 % от высоты конденсатной камеры ( 360 мм), в противном случае возникнет вероятность попадания жидкого конденсата в паропровод вторичного (сокового) пара, что приведет в свою очередь к нарушению давления в паропроводящей сети. Поэтому переходной процесс является граничным апериодическим без перерегулирования.
Рис. 23. Переходная характеристика объекта регулирования.
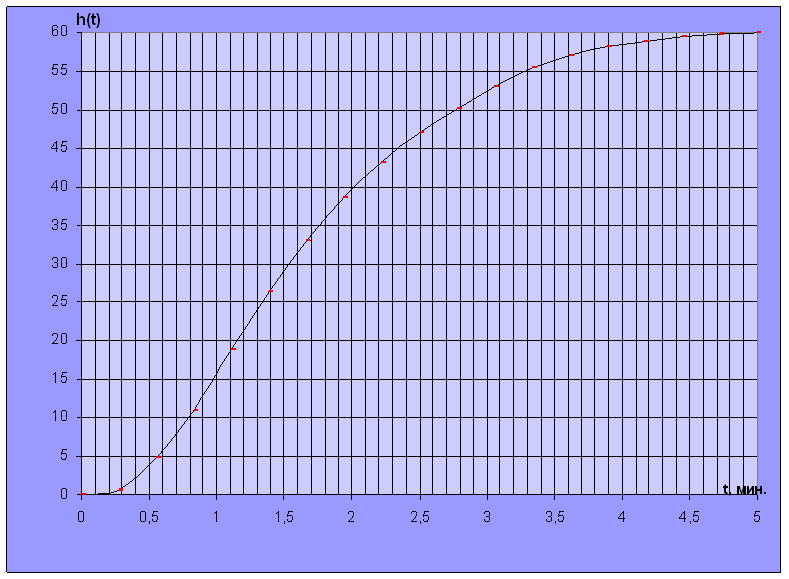
Для определения типа регулятора необходимо определить постоянную времени Т при
динамическом запаздывании τ =0,3333 мин.
В качестве передаточной функции объекта принимаем функцию, найденную методом интегральных площадей так как в данном случае погрешность аппроксимации переходной характеристики минимальна и составляет 5,927%.
Передаточная функция объекта имеет вид:
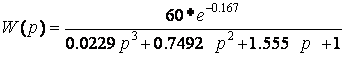
Для определения постоянных времени Т1, Т2, Т3 определим корни характеристического уравнения:
=0
При помощи программы Polinom. exe получим:
x0 = -30,53949
x1 = -1.1961722
x2 = -1.1961812
Для определения постоянной времени необходимо определить модуль комплексного корня:
Преобразуем полином следующим образом:
(p-p01)( p-p02) (p-p03)=0
,
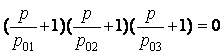где 
=Ti
Следовательно:
(p-p01)( p-p02) (p-p03)=(p+1.196172)(p+1.196181)(p+30,539)=(0.836p+1)(0.836p+1)(0.032p+1)
Таким образом передаточную функцию объекта можно представить в следующем виде:
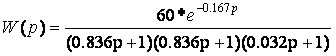
Для выбора типа регулятора принимаем Т = 0,836 мин.
Таким образом:
=
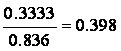> 0,2
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.