Другие предметы \ Автоматизация технологических процессов

Система автоматического регулирования уровня конденсата в конденсатоотводчике, страница 34

№ точки

40

41

t, мин

3,03439

4,83

lgF5

-0,5819

-0,364

Рис. 21. График функции “невязки” f 5.

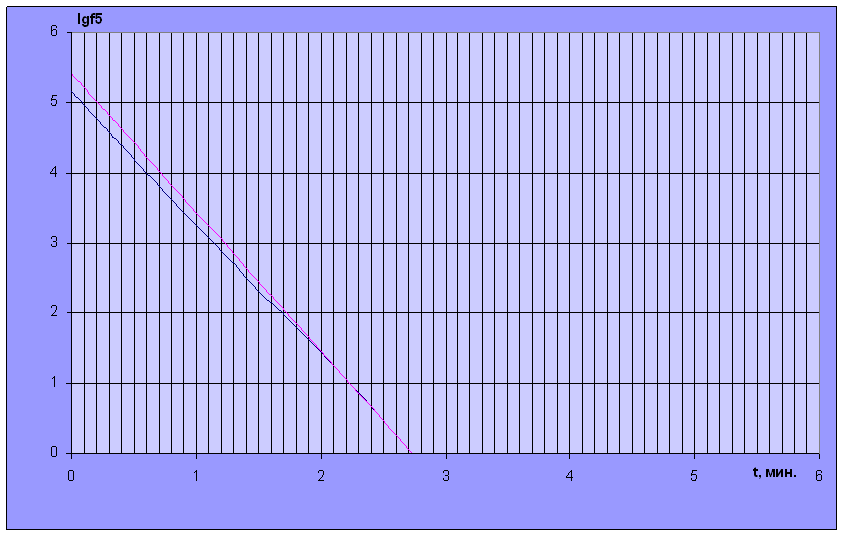
Проводим к хвостовой части касательную А5 этой точке соответствует значение lgC5=5.421,

откуда С5=263633.14.

 При этом t5=2.72 мин.

Определяем α5 как:

α5 =-lg[C5]/0.434*t5=-5.421/0.434*2.72=-4.592,

откуда 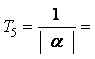1/4.592=0.21776 мин.

Следовательно, пятая составляющая суммы равна:

С5e-t/T5=263633.14*e-t/0,21776.

 При малых t lg [f5(t)]  практически совпадает с А5.

В результате обработки получена передаточная  функция пятого порядка m=5, при коэффициентах: С0=К=60, С1=323.59, С2=1698.2437, С3=11712.6455 , С4=131825.67, С5=263633.14;

и постоянных времени: Т1=0.7296 мин, Т2=0.3238 мин, Т3=0.2656 мин, Т4=0.2195 мин., Т5=0.21776 мин.

Таким образом переходная функция объекта имеет следующий вид:

h(t)=60-(323,59e-t/0,7296+1698,2437e-t/0,3238+

+11712.6455e-t/0.2656+131825,67e-t/0,2195+263633.14*e-t/0,21776)

Разделим все коэффициенты на С0, получим характеристику в относительном виде:

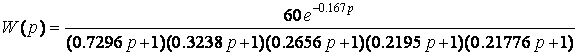
2.3.4. С помощью программы ASOTAR , введя параметры передаточной функции, найденные вышеприведенным методом, построим расчетную переходную характеристику. (Рис. 22)

Передаточная функция объекта имеет вид:

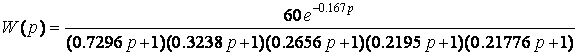
Рис 22. Расчетная переходная характеристика.

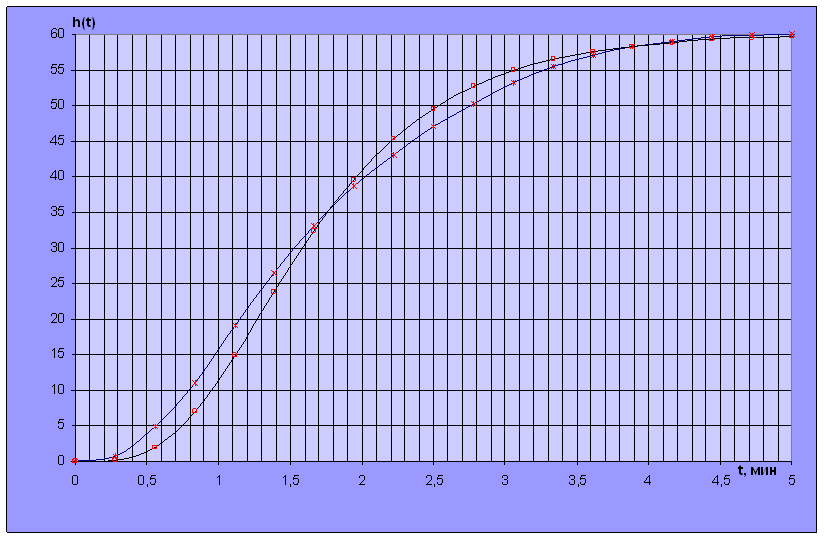
Таблица 2.14.                                                                                                                                                                                       

№ точки

1

2

3

4

5

6

7

8

9

10

11

t, мин.

0

0,2778

0,5556

0,8333

1,1111

1,3889

1,6667

1,9444

2,2222

2,5

2,77778

h(t)расч

0

0,1253

1,8861

6,9784

14,866

23,815

32,309

39,526

45,232

49,531

52,6678
Скачать файл