Решебник по физике. Части 1-3 "Термодинамика", "Статистическая физика" и "Физическая кинетика", страница 9

Максимальная работа, которую можно получить, равна

A = C₁T₁₀ + C₂T₂₀ – (C₁ + C₂).

Следует обратить внимание на то, что максимальная работа будет совершена в равновесном процессе. В этом случае суммарная энтропия нагревателя и холодильника неизменна, т. е. выполняется условие

Это условие эквивалентно написанному выше равенству Клаузиуса.

1.8. Температуры нагревателя R₁, природного резервуара воды R₂ и охлаждаемого резервуара R₃ считаем постоянными. Схема установки приведена на рисунке.

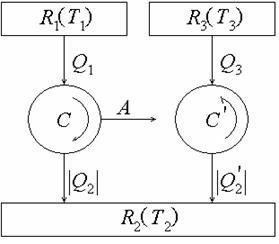
Для суммарного циклического процесса, совершаемого системой из двух рабочих тел,  можно написать неравенство Клаузиуса

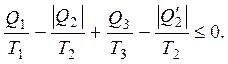
Его можно преобразовать к виду:

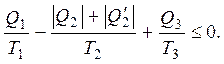
Сумма в числителе второго слагаемого в левой части неравенства находится из закона сохранения энергии. Этот закон можно сформулировать в различных формах. Первый вариант

[сумма всех теплот, полученных системой рабочих тел] = 0

или

Второй вариант – через равенство работы, совершаемой первым рабочим телом, значению работе внешних сил над вторым рабочим телом в течение цикла:

Откуда, независимо от варианта, получаем  Исключение этой суммы приводит к неравенству

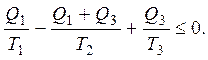
Из него следует ответ

Q₁ ≥ Q₃×T₁/T₃×(T₂ - T₃)/(T₁ - T₂) » 38 Вт.

1.9. В обычном способе отопления теплота, выделяющаяся при сгорании топлива, непосредственно поступает в отапливаемое помещение. Значительная доля этой теплоты уносится нагретыми газами и бесполезно расходуется на нагрев окружающей среды. Но даже если отвлечься от этой и других потерь, помещение при обычном способе обогрева получает теплоты не больше, чем выделяется при сгорании топлива. В задаче предлагается рассмотреть динамический способ отопления помещения.

При динамическом способе отопления только часть теплоты от сгорания топлива поступает в помещение, другая же часть расходуется на работу тепловой машины. С ее помощью приводится в действие холодильная машина, которая отбирает теплоту у окружающей среды и передает ее в помещение. Таким образом, помещение получает теплоту и от топки, и от холодной окружающей среды. Общее количество теплоты, получаемое помещением, может оказаться больше, чем выделяющееся при сгорании топлива. В этом выгода данного способа отопления. Он был предложен В. Томсоном.

Схематично динамический способ отопления изображен на рисунке. Пусть T₁, T₂ и T₃ – температуры  топки, помещения и окружающей среды соответственно. Количество теплоты, получаемое при сгорании  топлива, равно Q₁. Оно расходуется на работу A тепловой машины, часть его ÷Q₂÷  (Q₂ < 0) поступает в помещение. Очевидно,

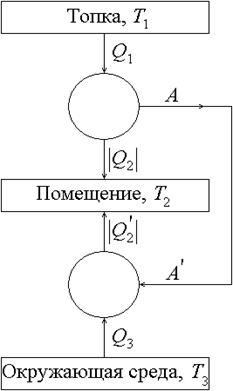A ≤ Q₁ – ÷Q₂÷

– из-за возможных потерь части тепла. Этой работой приводится в действие холодильная машина. Здесь возможны тоже потери на трение и т. д. Поэтому

A ≥ A'.

Холодильная машина отбирает от окружающей среды тепло Q₃ и передает помещению тепло ÷Q₂'÷ (Q₂' < 0; Q_i  без знака модуля обозначают теплоты, полученные рабочими телами обоих тепловых машин). Здесь имеет место неравенство

A' ≥ ÷Q₂'÷ – Q₃,

т.е. работа по отбиранию тепла от окружающей среды может оказаться больше расчетной по причине возможности действия в системе диссипативных сил. Из этих неравенств получается

Q₁ – ÷Q₂÷ ≥ ÷Q₂'÷ – Q₃, или Q₃ ≥ (÷Q₂÷ + ÷Q₂'÷) – Q₁.

В скобках стоит тепло, поступающее в отапливаемое помещение. Если для выражения в скобках ввести обозначение Q = ÷Q₂÷ + ÷Q₂'÷, то

Q₃ ≥ Q – Q₁.

Если теперь рассмотреть тепловую и холодильную машины как одну

термодинамическую систему, совершающую циклический процесс, то на основании неравенства Клаузиуса

Q₁ / T₁ + (Q₂ + Q₂') / T₂ + Q₃ / T₃ ≤ 0,