Решебник по физике. Части 1-3 "Термодинамика", "Статистическая физика" и "Физическая кинетика", страница 15

В этом случае система A¢может находиться только в пяти равновероятных доступных состояниях. Они перечислены в таблице.

№	s1	s2	s3	s¢1	s¢2	M	M¢
1	1	1	1	1	–1	3m0	0
2	1	1	1	–1	1	3m0	0
3	1	–1	–1	1	1	–m0	4m0
4	–1	1	–1	1	1	–m0	4m0
5	–1	–1	1	1	1	–m0	4m0

И в этих пяти состояниях магнитный момент первой системы может принимать только два значения: 3m₀ и –m₀. Вероятности этих двух значений равны w(3m₀) = 2/5 и w(–m₀) = 3/5 (число состояний с заданным магнитным моментом подсистемы поделить на число состояний, которые удовлетворяют фиксированному значению полной энергии системы, в данном случае  E₀ = –3m₀ B).

. Среднее значение магнитного момента этой подсистемы равно

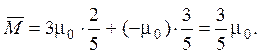
2.4. Энергия полной системы A + A¢ равна

E₀ = 3m₀B – 4m₀B = –m₀B.

При установлении равновесия полная система может находиться в любом из семи доступных состояний: (– – –, + +), (– + +, – +), (+ – +, – +), (+ + –, – +), (– + +, + –), (+ – +, + –), (+ + –, + –). Только в одном из них магнитный момент системы A равен –3m₀, в остальных шести он равен +m₀. Возможные значения этого момента не реализуются. Таким образом,

w(–3m₀) = 1/7, w(+m₀) = 6/7, w(+3m₀) = w(–m₀) = 0.

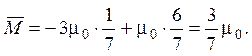
2.5. Наиболее вероятная скорость атомов идеального газа равна

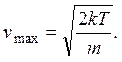
По условию задачи n×v_max = const. Откуда следует, что  или (с учетом того, что концентрация атомов n = N_А/V, где N_А – число Авогадро, V – молярный объем),  (A – постоянная). Для идеального газа теплоемкость

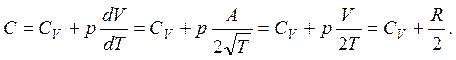
2.6. Распределение Максвелла для идеального газа в общем случае имеет вид

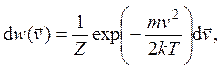
где  – элемент объема пространства скоростей, Z – статистический интеграл (нормировочная постоянная).

Для двумерного газа распределение принимает вид

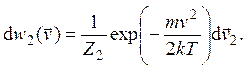
Здесь  – элемент объема двумерного пространства скоростей, а Z₂ – статистический интеграл двумерного газа, его значение находится из условия нормировки:

,

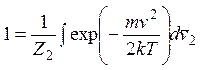где интегрирование проводится по всему доступному частице газа пространству скоростей.

Если в этом двумерном пространстве ввести декартовые координаты v_x и v_y, то элемент объема равен

Подставляя значение  в распределение, а также вычисляя нормировочную постоянную, получаем

dw(v_x, v_y) = m/2pkT×exp(– m(v_x² + v_y²)/2kT) dv_x dv_y,

Якобиан перехода от декартовых координат к полярным равен единице, поэтому, чтобы получить распределение в полярных координатах, достаточно в полученном распределении для декартовой системы координат выразить элемент объема в пространстве скоростей через переменные полярной системы координат. В полярных координатах v и j элемент объема в пространстве скоростей равен

Отсюда получаем:

dw(v, j) = ( m/kT×exp(– mv²/2kT) v dv×) (dj/2p) = dw(v)dw(j),

где dw(v) и dw(j) – нормированные распределения по модулю скорости vи углу j:

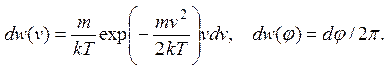
Средняя энергия молекулы идеального двумерного газа равна

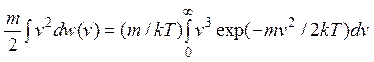= m/2 = = kT.

Замечание. Интеграл может быть вычислен методом дифференцирования по параметру:

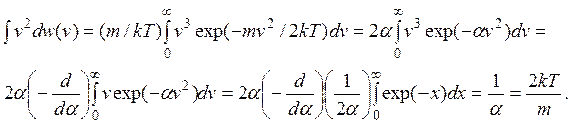
2.7. Распределение Максвелла для идеального двумерного газа имеет вид

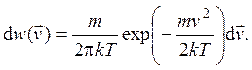
Здесь  – элемент объема двумерного пространства скоростей. Если в этом пространстве выразить элемент объема через полярные координаты и проинтегрировать по угловой координате, получим распределение по величине скорости (см. задачу 2.6)

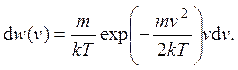
Средняя скорость теплового движения молекул двумерного газа равна