Итак, (¶CV/¶V)T = T(¶2p/¶T 2)V. Для газа Ван-дер-Ваальса (p = nRT/(V – bn) – an2/V2) легко показать, что вторая производная от давления по температуре при постоянном объеме равна нулю, т. е. CV не зависит от объема, а является функцией только температуры.
Из приведенных выше соотношений можно найти частные производные от энтропии (ниже CV – молярная теплоемкость):
(¶S/¶T)V = nCV(T)/T, (¶S/¶V)T = (¶p/¶T)V = nR/(V – bn)
и
dS = (¶S/¶T)VdT + (¶S/¶V)TdV = nCV(T)dT/T + nRdV/(V – bn).
Интегрирование последнего равенства дает энтропию:
S = n(
dT/T + R×ln(V/n
- b) + const).
Из основного термодинамического тождества следует:
dU = TdS – pdV = CV(T)dT + an2dV/V2.
Интегрирование дает внутреннюю энергию:
U = n(dT - an/V
+ const).
Замечание. Пропорциональность постоянных интегрирования числу молей определяется требованием на аддитивность энтропии и внутренней энергии. Действительно, выражение в скобках зависит только от интенсивных или удельных параметров: температуры и удельного объема V/n.
1.17. Свободное расширение – это процесс Гей-Люссака, т. е. без подвода теплоты Q = 0 и совершения работы A¢ = 0, с сохранением внутренней энергии DU = 0. В предыдущей задаче было получено выражение для внутренней энергии газа Ван-дер-Ваальса. Используя его, сохранение внутренней энергии в рассматриваемом процессе можно записать в виде равенства
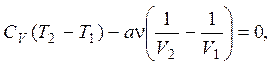
откуда находится искомая постоянная
a = CV(T2 – T1)V1V2/(ν(V1 – V2)) ≈ 0,42 Дж∙м3/моль2.
1.18. Поскольку подвода тепла нет и работа внешних сил отсутствует, то внутренняя энергия системы остается такой же, какой была вначале, до установления контакта между кубиками:
DU = mСV (T– T1 ) + mСV (T– T2 ) = 0.
Это позволяет сразу же найти конечную температуру кубиков:
Т = (Т1 + Т2)/2.
При этом используется равенство масс кубиков, учитывается, что CV = const. Изменением объема кубиков пренебрегается.
Изменение энтропии не зависит от процесса. Реальный процесс для каждого кубика заменяется изохорическим. В этом процессе энтропия кубика меняется с температурой по закону
S = S0
+ 
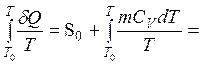S0 + mcv×ln(T/T0),
где S0 – значение энтропии при температуре Т0 (оно одно и то же для обоих кубиков, так как кубики одинаковы). На T, S-диаграмме точка (T0, S0) вводится как общая точка отсчета. На результат она не влияет. Тогда с учетом аддитивности энтропии ее изменение для системы равно
DS = DS1 + DS2 = ΔS = mcv×ln((T1 + T2)2/4T1 T2) > 0.
Энтропия адиабатически изолированной системы кубиков в результате установления теплового равновесии возросла. Изменение свободной энергии системы равно
DF =DU – (T×2S – T1S1
– T2S2) = mcv×ln(
).
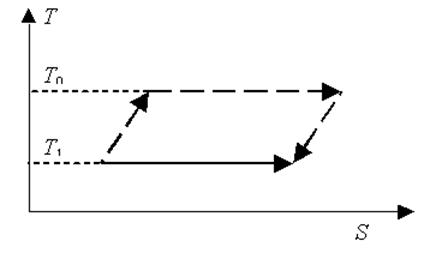
1.19. Изменение энтропии не зависит от пути перехода системы из одного состояния в другое. На этом основании изменение энтропии в результате плавления вещества при температуре T1 можно приравнять изменению энтропии в следующем переходе. Вначале твердое вещество нагревается от температуры T1 до T0, затем происходит его плавление при температуре T0 (а при этой температуре теплота плавления вещества известна), и, наконец, уже в жидком состоянии вещество охлаждается от T0 до T1. На T,S – диаграмме изображены: сплошной линией – путь перехода при температуре T1 < T0, пунктиром - предложенный путь перехода, изменение энтропии на котором мы будем определять.
Подсчитать изменение энтропии при таком переходе несложно:
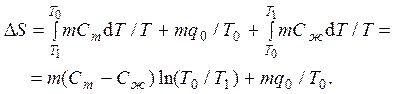
С другой стороны, то же изменение энтропии в результате плавления вещества при температуре T1 равно
Приравнивание этих двух выражений для DS дает
1.20. Изменение энтропии системы при переходе малого количества теплоты Q от одного тела к другому равно
ΔS= Q / T1 – Q / T2.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.