Решебник по физике. Части 1-3 "Термодинамика", "Статистическая физика" и "Физическая кинетика", страница 7

Эта сила является геометрической суммой сил, действующих на поршень с обеих сторон. Так как давление газа всегда направлено по внутренней нормали к поверхности объема, внутри которого заключен газ, то сила, вызванная давлением p₀, сонаправлена оси x, а сила, вызванная давлением p, имеет направление, противоположное оси x. Учитывая адиабатичность процесса в замкнутой части объема, можно записать следующее соотношение:

где V – объем закрытой части цилиндра.

Так как V = V₀ – Sx, то

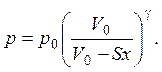
Учитывая малость колебаний и разлагая p в ряд Тейлора по степеням x, получаем:

p = p₀(1 + gSx/V₀);

p₀ – p =  – p₀gSx/V₀.

Тогда второй закон Ньютона для поршня имеет вид:

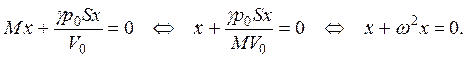
Отсюда, частота колебаний

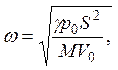
а период

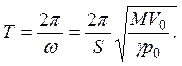
1.3. С учетом того, что поршни тяжелые (m_газа << m₁, m₂), следует записать законы сохранения импульса и энергии:

,

,

Или

.

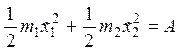Обозначения в уравнениях соответствуют рисунку.

 В условии задачи сказано, что поршни «тяжелые». Из этого следует, что скорость их движения достаточно мала для того, чтобы адиабатическое расширение газа в от конечного объема V₀ до бесконечности происходило равновесно. В этом случае работу газа A можно найти как работу при равновесном адиабатическом процессе:

.

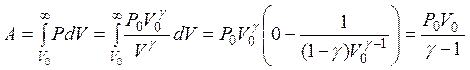С учетом выражения для работы имеем систему уравнений:

.

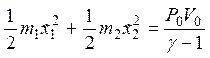Решение системы уравнений дает:

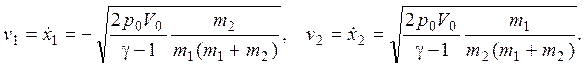
1.4. В первое начало термодинамики входит величина Q. Под ней понимают количество теплоты, полученное системой. По условию задачи «уходящее тепло равно изменению внутренней энергии газа» –­ поэтому в соотношении между Q и DU возникает знак «минус»:

Q = –DU.

Так как газ идеальный, то его внутренняя энергия – функция только температуры. Пусть теплоемкость C_Vпостоянна. Тогда

Q = – C_V(T – T₀).

Здесь либо C_V теплоемкость всего газа, либо количество газа равно одному молю, и тогда C_V – молярная теплоемкость. Таким образом, теплоемкость газа в рассматриваемом процессе равна

.

Работа, совершаемая над газом, и подведенная к нему теплота идут на изменение его внутренней энергии (первое начало термодинамики). Для условий задачи

A'^¢ = DU – Q = 2DU = 2C_V (T – T₀).

Для нахождения конечной температуры необходимо получить уравнение процесса. С этой целью рассматривается первое начало термодинамики в дифференциальной форме. Для данной задачи оно имеет вид

– dU = dU + pdV.

Слева – количество теплоты, полученное газом. Для идеального газа уравнение можно преобразовать:

2dU + pdV = 0    Þ    2C_V dT + RTdV/V = 0.

Оно решается разделением переменных, так что

где g – показатель адиабаты. По условию газ сжимается с уменьшением объема в два раза. Окончательно

1.5. Так как система теплоизолирована, то согласно первому началу, работа внешних сил приводит к изменению внутренней энергии системы:

A'^¢ = DU₁ + DU₂.

Предполагается, что поршень перемещается без трения.

Для идеального газа бесконечно малое изменение внутренней энергии равно dU = nC_V dT. Если теплоемкость C_V считать постоянной, то конечное изменение U равно

DU = nC_V (т – т₀) = nC_V т₀( т /T₀ – 1) = P₀V₀ ( т /T₀ – 1) /(g – 1),

где Т₀ – начальная температура газа.

а) Так как поршень перемещается медленно и не проводит тепло, то изменение объема газов в каждой из частей сосуда – адиабатические процессы. Уравнение адиабаты для идеального газа было получено в задаче 1.1: pV^g = const. В переменных T, V оно имеет вид:

тV^{g – 1} = const.

Пользуясь им, получаем конечные температуры газов:

T₁ = T₀(V₀/V₁)^{g – 1} = 2^{g – 1}, T₂ = T₀(V₀/V₂)^{g – 1} = (2/3)^{g – 1}.

Работа внешних сил в этом случае равна

A¢ = DU₁ + DU₂ = p₀ V₀/(g – 1)×(2^{g –  1} + (2/3)^{g – 1} – 2).

б) В случае теплопроводящего поршня температуру газа в обеих частях сосуда можно считать одинаковой в любой момент времени. Одинаково также число молей газа. Это следует из начальных данных. В результате