Решебник по физике. Части 1-3 "Термодинамика", "Статистическая физика" и "Физическая кинетика", страница 18

2.18. В соответствии с условиями задачи молярная теплоемкость при постоянном объеме двухатомных газов на нижней температуре равна C_V = 5R/2. В результате реакции температура газовой смеси существенно повышается, и происходит возбуждение колебательного движения молекул. Молярная теплоемкость при постоянном объеме двухатомных газов становится раной C_V = 7R/2.

Запишем закон сохранения энергии для рассматриваемой реакции

H₂ + F₂ → 2HF

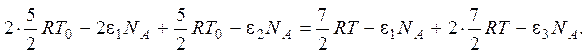
Слагаемые с e_i (i – 1-3) учитывают введение одного уровня отсчета энергии для разных молекул (двухатомная молекула по сравнению с парой соответствующих атомов при одной и той же температуре обладает отрицательной энергией). Из закона сохранения энергии находится температура газовой смеси после завершения реакции

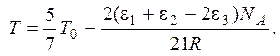
2.19. Статистическая сумма двумерного осциллятора вычисляется с помощью дифференцирования по параметру α = hn/kT

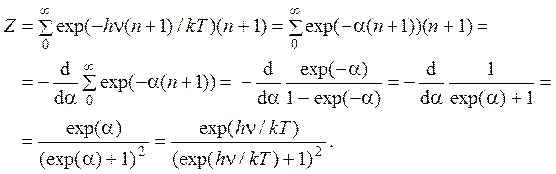
Отсюда

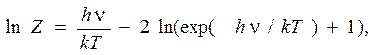
и по формуле, полученной в задаче 2.15

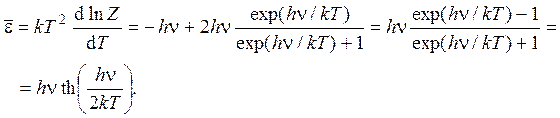
Энергия и теплоемкость системы из N двумерных осцилляторов равны соответственно

Е = Nhn×cth(hn/2kT),   C_V = 2Nk (hn/2kT)²/sh²(hn/2kT).

2.20. Для жесткой двухатомной молекулы вращательные энергетические уровни имеют спектр

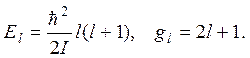
Здесь l – орбитальное квантовое число, g_l – кратность вырождения уровней, I = ma²– момент инерции молекулы, m = m₁m₂/(m₁ + m₂) – приведенная масса.

Распределение Больцмана дает населенность вращательных уровней

Определяется экстремум этой функции

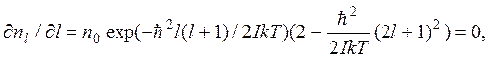
откуда

Расчет для условий задачи дает

m = 1.15×10^–23 г, I = 1.47×10^–39 г×см², l_max = 6.

2.21. Вероятность обнаружить систему в состоянии с той или иной энергией определяется распределением Гиббса:

w_i = exp(–e_i/kT)g_i/( exp(–e₀/kT)g₀ + exp(–e₁/kT)g₁),   i = 0, 1.

Средняя энергия системы по определению равна

Тогда теплоемкость вычисляется по формуле:

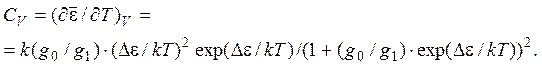
т.е. C_V ® 0 при Т ® 0. Энергия теплового движения мала, чтобы возбудить состояния с энергией e₁. При Т >> De/kT C_V = kg₀g₁/(g₀ + g₁)²(De/kT)². В пределе Т ® ¥ теплоемкость также стремится к нулю. Все состояния системы возбуждены. График зависимости теплоемкости от температуры имеет максимум.

Населенность уровня из определения вероятности равна

N_i = Nw_i,   i = 0, 1.

2.22. В магнитном поле напряженности н молекула вещества приобретает потенциальную энергию –mн, где m может иметь три значения: m = m₀×m, m = 0, ±1. Соответственно этому магнитное триплетное состояние распадается на три, и спектр энергий имеет вид, показанный на рисунке.

Намагниченность представляет собой суммарный магнитный момент молекул единицы объема вещества:

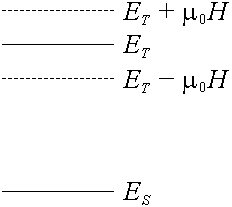M = Sm_in_i,

где m_i – проекция на направление поля магнитного момента молекулы, находящейся на i-ом уровне энергии; n_i – концентрация таких молекул.

Величина их определяется распределением Гиббса

Здесь n – полная концентрация молекул, Е_i – энергия уровня (с учетом расщепления статистический вес уровней равен единице); Z –статистическая сумма. Последняя находится из условия нормировки:

Z = Sexp(–E_i/kT).

После подстановки n_i выражение для намагниченности преобразуется к виду

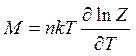
Для данной задачи статистическая сумма равна

Z = exp(–Е_S/kТ) + exp(–(Е_T – m₀H)/kТ) + exp(–Е_T/kТ) + exp(–(Е_T + m₀H)/kТ).

Путем дифференцирования Z по Н находится намагниченность

M = nm₀(exp(m₀H/kТ) – exp(–m₀H/kТ))/(exp(DЕ/kТ) +

+ exp(m₀H/kТ) + 1 + exp(–m₀H/kТ))

Обычно реализуются условия, при которых параметр m₀H/kТ << 1. Если провести разложение по этому параметру, то для намагниченности получается выражение

M = 2nm₀²H/kT/(exp(DЕ/kТ) + 3).

Магнитная восприимчивость равна

c = М/Н = 2nm₀²/kT/(exp(DЕ/kТ) + 3).

Замечание. Решение задачи получено для изотропного магнетика.