Решебник по физике. Части 1-3 "Термодинамика", "Статистическая физика" и "Физическая кинетика", страница 8

А' = DU₁ + DU₂ = 2nC_V (т – т₀) = 2P₀V₀ ( T/T₀ – 1)/( g – 1).

Конечная температура системы может быть найдена из уравнения процесса. Для получения уравнения процесса первое начало термодинамики записывается в дифференциальной форме для всей системы:

2dU + p₁dV₁ + p₂dV₂ = 0.

Если подставить сюда выражение для dU через температуру и теплоемкость ( dU = nC_V dT ), выразить давление с помощью термического уравнения состояния идеального газа ( p =nRT/V ) и затем поделить все слагаемые на 2nC_V т, то дифференциальное уравнение примет вид

dT /Т + (g – 1)/2×(dV₁/V₁ + dV₂/V₂) = 0.

При преобразовании используются соотношение Майера C_p – C_V = R и показатель адиабаты g = C_p/C_V. Интегрирование дает уравнение процесса:

ln(Т/Т₀) + (g – 1)/2× ln(V₁V₂/V₀²) = 0.

Найдем значения экспоненты с показателями, равными правой и левой части уравнения. Получим равенство:

Т/Т₀ = ( V₀²/ V₁V₂) ^{(g – 1)/2}

Конечная температура системы равна

Т = Т₀ (4/3)^{(g – 1)/2}.

Работа внешних сил

А' = 2P₀V₀ ( T/T₀ – 1)/( g – 1) = 2p₀V₀/(g – 1) ((4/3)^{(g – 1)/2} – 1).

1.6. По определению теплоемкости и с учетом первого начала термодинамики для идеального газа

C = ¶Q/¶T = ¶U/¶T + p¶V/¶T = C_V + p¶V/¶T.

По условию задачи объем газа V = Sx (x – сжатие пружины, S – площадь поршня) и Sp = kx (поршень удерживается пружиной, см. рисунок ниже),

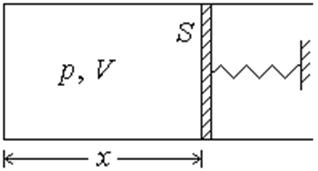откуда

V = Sx = S (Sp/k ) = const×p.

Логарифмирование и дифференцирование дает:

d ( ln (V =const×p ))  Þ dV/V = dp/p.

Аналогично из термического уравнения состояния можно получить

d ( ln (p = RT/Vp ))  Þ dp/p + dV/V = dT/T.

Из двух полученных уравнений находится производная

¶V/¶T = V/2T,

так что

C = C_V + p¶V/¶T = C_V + p V/2T = C_V + R/2 = 2R.

(для одноатомного газа C_V  = 3 R/2).

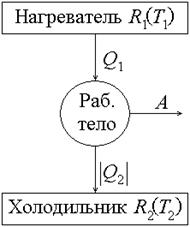
1.7. Максимальная работа будет получена, если использовать тепловую машину, работающую по обратимому циклу Карно. Схема такой машины приведена на рисунке.

Однако теплоемкости тел (нагревателя и холодильника) в данной задаче конечные, и их температуры при тепловом контакте с рабочим телом тепловой машины в общем случае изменяются. Поэтому для получения максимальной работы применятся непрерывная последовательность бесконечно малых циклов Карно, в пределах каждого из которых текущие температуры тел Т₁ и Т₂ (соответственно температуры нагревателя и холодильника) можно считать постоянными. При контакте с нагревателем (тело 1) рабочее тело получает количества тепла, равное dQ₁ . Это тепло dQ₁, согласно рисунку, является «отданным теплом» для нагревателя (тела 1). Другими словами, нагреватель получает тепло, равное

– dQ₁ = C₁ dT₁.

От холодильника (тело 2), согласно введенным обозначениям, рабочее тело получает тепло, равное  – dQ₂ . В то же время холодильник (тело 2) получает тепло, равное

dQ₂ = C₂ dT₂.

Таким образом, тепловая машина будет совершать работу за счет внутренней энергии тел 1 и 2. Совершаемая за цикл работа равна сумме теплот, полученных рабочим телом в течение цикла

dА = dQ₁ – dQ₂ = – C₁dT₁ – C₂dT₂.

Работа машины продолжается до тех пор, пока температуры тел не становятся равными: T₁ = T₂ = Т. Полная работа равна

А = C₁T₁₀ + C₂T₂₀ – (C₁ + C₂)Т.

Для нахождения конечной температуры тел можно воспользоваться равенством Клаузиуса для обратимого цикла:

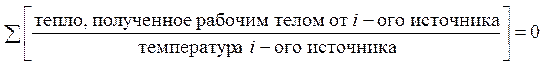
dQ₁/T₁ – dQ₂/T₂ = 0  Þ  C₁dT₁/T₁ + C₂dT₂/T₂ = 0.

Заметим, что знаки перед dQ₁  и dQ₂ стоят те же самые, что и в выражении для работы, совершаемой в цикле – действительно, в обоих случаях фигурирует тепло, полученное рабочим телом. Интегрирование последнего равенства дает конечную температуру: