Решебник по физике. Части 1-3 "Термодинамика", "Статистическая физика" и "Физическая кинетика", страница 10

и с учетом того, что Q₂ = – ÷Q₂÷ и Q₂' = – ÷Q₂'÷, получается

Q₁ / T₁ – (÷Q₂÷ + ÷Q₂'÷) / T₂ + Q₃ / T₃ ≤ 0,

или

Q₁ / T₁ – Q / T₂ + Q₃ / T₃ ≤ 0.

Исключение Q₃ дает

Q₁ / T₁ – Q / T₂ +  (Q – Q₁)  / T₃ ≤ 0,

откуда

Q ≤ (T₃^–1 – T₁^–1)  /  (T₃^–1 – T₂^–1)  × Q₁.

В идеальном случае, когда какие-либо потери теплоты или работы отсутствуют и все процессы квазистатические, имеет место равенство

Q = (T₃^–1 – T₁^–1)  /  (T₃^–1 – T₂^–1)  × Q₁.

Так как T₁ > T₂, то T₃^–1 – T₁^–1 > T₃^–1 – T₂^–1 и полученная формула дает Q > Q₁. Более того, разница температур T₂ и T₃ сравнительно небольшая (до нескольких десятков градусов), тогда как T₁ значительно больше T₂ (на  сотни градусов). Поэтому множитель перед Q₁ может быть порядка 10. Это говорит об эффективности динамического способа отопления.

Для условий задачи Q/Q₁ = (T₁ – T₃)T₂/(T₂ – T₃)/T₁ ≈ 7,1.

1.10. Процесс Гей-Люссака – это расширение газа в пустоту.

Пусть сосуд с жесткими адиабатическими стенками разделен перегородкой на объемы V₁ и V₂. В первом объеме ν молей идеального газа при температуре T, в другом объеме – вакуум. Перегородка убирается – газ приходит в движение и заполняет весь объем сосуда V₁ + V₂. Это процесс Гей-Люссака.

Конечное состояние газа при его расширении равновесное. Подвода теплоты нет: Q =  0. Работа внешних сил отсутствует: A' = 0  (стенки сосуда жесткие). Внутренняя энергия газа в результате не изменится: ΔU = 0. А так как газ идеальный, то в соответствии  с законом Джоуля конечная температура равна начальной температуре. Сразу же следует сделать уточнение. В процессе расширения говорить о температуре газа как целого не имеет смысла. Это неравновесный процесс, что подтверждается тем, что его конечным результатом является увеличение энтропии газа, несмотря на отсутствие подвода теплоты. Процесс протекает с конечными скоростями. Внутренняя энергия газа в процессе не остается постоянной. Она переходит в кинетическую энергию поступательного движения газа. Происходит это неравномерно. Уже с самого начала одни слои газа приходят в движение, другие еще неподвижны. Все же в конце концов кинетическая энергия движущегося газа диссипирует и переходит во внутреннюю энергию, устанавливается равновесие. Поскольку процесс неравновесный, то пользоваться непосредственно уравнением dS = δQ / T нельзя: оно справедливо только для равновесных процессов. Однако энтропия – функция состояния, ее изменение не зависит от процесса. Путей решения задачи два: можно воспользоваться известным выражением для энтропии идеального газа и по начальному и конечному состояниям вычислить ее изменение. А можно реальный (неравновесный) процесс, соединяющий два равновесных состояния, заменить подходящим равновесным, соединяющим те же два равновесных состояния (в данном случае самым простым  из подходящих процессов является изотермический) и искать изменения энтропии согласно формуле dS = δQ / T в построенном равновесном процессе . Здесь рассматривается второй путь.

Вводится изотермический процесс перехода из начального состояния с объемом V₁ в конечное состояние с объемом V₁ + V₂. В этом процессе в отличие от реального процесса есть подвод теплоты от термостата с температурой T. Эта теплота расходуется на работу газа – изотермическое расширение. В результате

ΔS =  =  = = 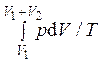= 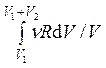νR·ln (1 + V₂ / V₁) > 0.

Возрастание энтропии указывает, что расширение в пустоту действительно неравновесный процесс.