Решебник по физике. Части 1-3 "Термодинамика", "Статистическая физика" и "Физическая кинетика", страница 21

t2prl|_r – t2prl|_r + dr + Dp2prdr = 0.

Сократив на 2p и разделив на ldr, получим дифференциальное уравнение

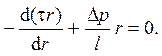
Напряжение трения для рассматриваемой задачи имеет вид

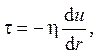
где h – коэффициент вязкости. После подстановки t получаем дифференциальное уравнение для скорости жидкости u

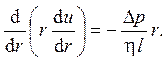
Для его решения имеются два граничных условия:

údu/drú < ¥ при r = 0 (на оси симметрии);

u = 0 при r = R (условие прилипания на стенке).

На оси симметрии обычно пишут условие симметрии du/dr = 0 при r = 0. Однако, в случае осесимметричной задачи достаточно использовать ограниченность производной. Однократное интегрирование с использованием первого условия дает

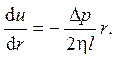
Последующее интегрирование с использованием второго условия дает параболический профиль скорости

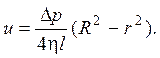
Он изображен на рисунке.

Расход жидкости определяется выражением

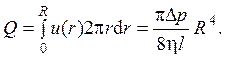
Это формула Пуазейля, а рассмотренное течение называется течением Пуазейля.

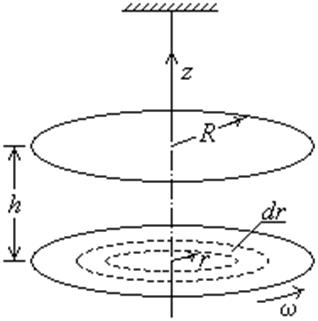
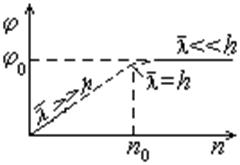
3.8. Пренебрежение краевыми эффектами означает, что весь момент импульса, получаемый газом между дисками от нижнего из них, передается верхнему диску, приводя его к повороту на угол j. Решение задачи оказывается различным при высоких и низких давлениях газа. Промежуточное давление определяется из условия равенства длины свободного пробега молекул расстоянию между дисками. Из равенства  следует, что

При низких давлениях (p << p₀) молекулы газа друг с другом практически не сталкиваются и переносят момент импульса от нижнего диска к верхнему непосредственно. Если считать, что, ударяясь о диск, молекула приобретает момент импульса, равный mur = mωr² (u = ωr – линейная скорость), и кроме того, вспомнить, что о единицу площади в единицу времени ударяется  молекул, то полный момент импульса, передаваемый от нижнего диска верхнему, равен

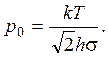
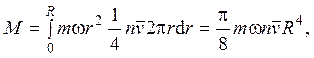
так что

оказывается прямо пропорциональным плотности, и следовательно, давлению газа. Для заданных условий

j = wR⁴/(a)×p » 0,015 рад.

При высоких давлениях (p >> p₀) справедлива гипотеза локального равновесия. Внутри газа возникают вязкие силы. На единичную площадку в сечении, параллельном дискам, действует сила

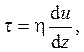
где u = ωr, ось координат z направлена от верхнего диска к нижнему диску. Можно показать, что скорость вращения газа зависит от z линейно. На верхнем диске она равна нулю, на нижнем диске – его угловой скорости ω. Поэтому τ = η ωr/l. Момент вязких сил, действующий на верхний диск, равен

Поскольку коэффициент вязкости η от давления не зависит, то и угол поворота j = pηωR⁴/(2la) не меняется с давлением. Расчет для условий задачи дает j = 81°. Зависимость угла поворота верхнего диска от концентрации газа качественно показана на рисунке.

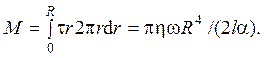
3.9. Размеры отверстия малы по сравнению с длиной свободного пробега:

.

Молекулы пролетают через отверстие, не испытывая столкновений друг с другом. Потоки молекул различных газов не связаны друг с другом. Изменение числа частиц одного газа в сосуде равно разности влетающих и вылетающих частиц этого газа. Снаружи гелий отсутствует. Поэтому балансовое уравнение для гелия имеет вид:

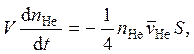
где  – концентрация и средняя скорость атомов гелия в сосуде. Сосуд тонкостенный, поэтому температуру гелия можно считать постоянной и равной температуре наружного воздуха. Уравнение решается методом разделения переменных:

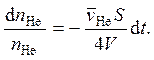
Начальное условие: n_не = n₀ при t = 0. Решение имеет вид:

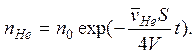
Уравнение состояния р = nкТ. Парциальное давление гелия в сосуде

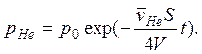
Для воздуха в балансовом уравнении необходимо учитывать как влетающие, так и вылетающие молекулы:

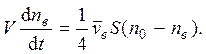
Оно также решается методом разделения переменных при условии: начальная концентрация молекул воздуха в сосуде равна нулю.

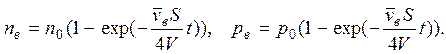
Суммарное давление в сосуде определяется законом Дальтона:

p = p_He + p_в.

Окончательно

р = р₀ (1 + exp(– t/t_He) – exp(– t/t_возд)),   t = 4V/(s).