Решебник по физике. Части 1-3 "Термодинамика", "Статистическая физика" и "Физическая кинетика", страница 16

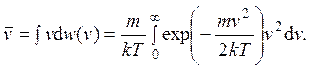
Интеграл вычисляется с помощью дифференцирования по параметру  α  (α = m/2kT):

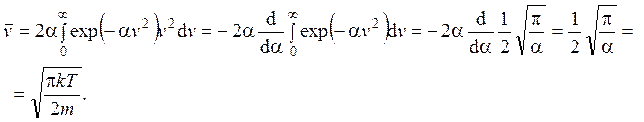
2.8. Прежде всего, заданное распределение следует нормировать. Для этого оно записывается следующим образом

dj = Aexp(–v/v₀)dv.

Постоянная A, входящая в это выражение, находится по известной мощности источника j:

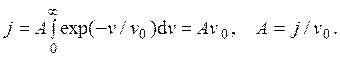
Давление двумерного газа, оказываемое молекулами со скоростью v на окружность – это импульс, получаемый от этих молекул единицей длины окружности в единицу времени. Каждая молекула со скоростью v передает импульс mv, всего таких молекул в единицу времени на единицу длины падает dj/2pR, так что полный передаваемый импульс или давление равно произведению этих величин:

.

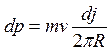Чтобы определить полное давление, оказываемое всеми молекулами, необходимо проинтегрировать по скоростям (интеграл вычисляется с помощью дифференцирования по параметру α = 1/v₀):

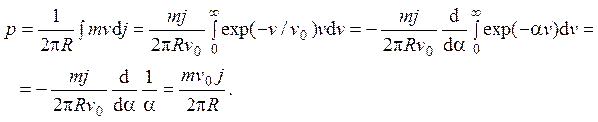
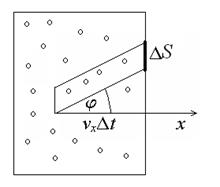
2.9. Пусть в некоторой области на плоскости находится идеальный двумерный газ при температуре T. На рисунке двумерная область изображена схематически прямоугольником, а молекулы – окружностями малого радиуса. Эти молекулы движутся хаотически в соответствии с распределением Максвелла. Через участок длиной DS границы области за малый промежуток времени Dt пролетят все молекулы со скоростью , которые в момент времени t =0 находились в параллелограмме с основанием DS и стороной, равной vdt и сонаправленной со скоростью молекул .

Количество подобных молекул dN равно произведению объема косоугольного цилиндра V на концентрацию подобных молекул в этом цилиндре dn(), или

.

В приведенной формуле dw() – максвелловская вероятность иметь скорость , а n – полная концентрация молекул в сосуде.

Плотность потока вылетающих через малое отверстие DS молекул с данной скоростью равна

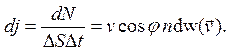
Плотность потока всех вылетающих молекул равна

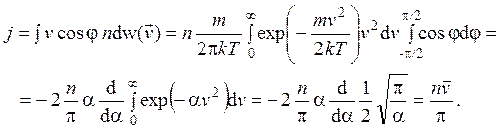
2.10. Распределение молекул по величине скорости в пучке имеет вид:

dw(v) = 2a²exp(–av²)v³dv,

где a = m/2kT.

По определению средних:

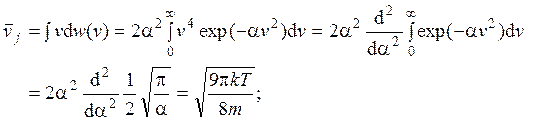
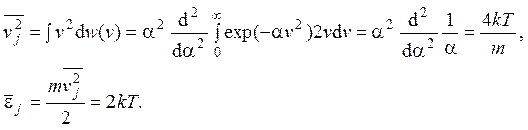
Средняя энергия молекул в пучке больше, чем в сосуде. Это вызвано тем, что молекулы с более высокими скоростями вылетают из большего объема (см. задачу 2.10 – объем косоугольного цилиндра пропорционален модулю скорости молекулы), поэтому их доля в пучке больше, чем в сосуде.

2.11. Импульс, передаваемый пластинке одной молекулой при упругом отражении, равен 2mv_x, где ось х направлена перпендикулярно плоскости пластинки. Если dj(v_x, v_^) – число молекул, падающих на. единицу площади пластинки в единицу времени и имеющих данные компоненты скорости v_x и v_^ (v_^ – составляющая скорости, перпендикулярная оси х), то сила, действующая на пластинку, равна

Для dj имеет место выражение: , где n – концентрация частиц в сосуде,  – распределение Максвелла (a = m/2kT). В цилиндрических координатах  Поэтому

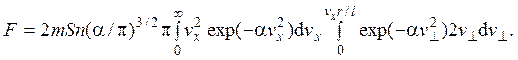
Очевидно, не все молекулы с данной v_х попадают на пластинку, а только те, у которых v_^ £ v_xr/l. Интегрирование дает окончательный результат

F = nkTs(1 – (1 + (r/l)²)^–3/2).

2.12. Скорость сосуда находится из закона сохранения импульса

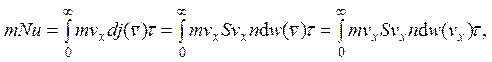
где m – масса молекулы, N – число их в сосуде, u – приобретенная сосудом скорость, S – площадь отверстия, n – концентрация молекул в сосуде. Пределы интегрирования указаны для проекции скорости на ось x. В силу того, что

,

а интегралы по вероятностям, связанные с проекциями скорости на ось z и y, равны единицам, зависимость от этих координат не фигурирует в конечном выражении.

 Предполагается, что отверстие открывается на столь малое время t, что равновесное состояние газа в сосуде не изменяется. Полное число молекул в сосуде связано с их концентрацией формулой N = nV (V – объем сосуда).

После исключения числа частиц N для скорости сосуда получаем

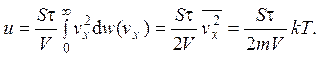
Здесь использован закон равнораспределения энергии по степеням свободы.