Решебник по физике. Части 1-3 "Термодинамика", "Статистическая физика" и "Физическая кинетика", страница 17

2.13. В соответствии с  распределением Больцмана концентрация молекул водорода и углекислого газа меняется с высотой по формуле

n_i = n_i0 exp(–m_igh/RT),

где i = 1, 2 (соответственно для H₂ с m₁ = 2 и CO₂ с m₂ = 44).

Изменение относительного содержания H₂ и CO₂ с высотой будет определяться равенством

n₁/n₂ = n₁₀/n₂₀ exp((m₂ – m₁)gh/RT),

откуда

2.14. В лабораторной системе отсчета газ в центрифуге вращается как единое целое, стало быть, имеется центростремительное ускорение, т. е. система не находится в механическом равновесии и к ней нельзя применить распределение Больцмана. В системе же отсчета, связанной с центрифугой, объект исследования находится в равновесии, и к нему можно применить указанное распределение. Но в этой системе отсчета на частицы действует центробежная сила. Соответствующая потенциальная энергия частицы равна

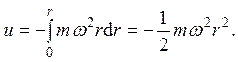
Распределение Больцмана с учетом цилиндрической симметрии имеет вид

где l – высота барабана центрифуги. Выражение для статистической  суммы получается из условия нормировки распределения

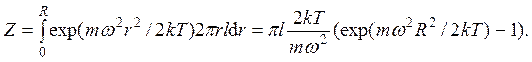
В результате для концентрации частиц получается формула

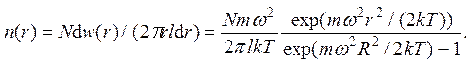
Из формулы следует, что концентрация тяжелых частиц у боковой стенки центрифуги относительно выше, что используется для разделения смесей. Концентрация частиц у боковой стенки центрифуги  равна

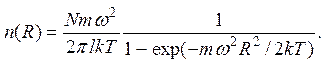
Соответствующее отношение концентраций молекул D₂ и H₂ будет

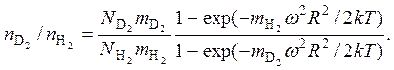
С учетом того, что масса молекулы дейтерия в два раза тяжелее и начальная пропорция изотопов водорода D₂ и H₂ равна b, при отборе смеси у боковой стенки центрифуги можно увеличить долю дейтерия

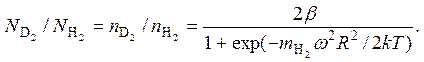
Максимальное соотношение компонент в смеси равно

2.15. Пусть для определенности спектр энергии системы непрерывный. Распределение Гиббса для нее будет

dw = 1/Z×exp(–e/kT)dG/h^f,

где dG – элемент объема фазового пространства, h^f – объем этого пространства, отвечающий одному состоянию системы (h – постоянная Планка, f – число степеней свободы системы). Статистическая сумма Z находится из условия нормировки

Интегрирование выполняется по всему доступному объему фазового пространства.

По определению, средняя энергии системы равна

Использование техники дифференцирования по параметру позволяет получить искомую формулу:

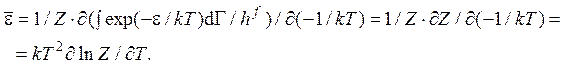
Эта формула остается в силе, если спектр энергии дискретный. Она применима также в случаях распределений Максвелла и Больцмана.

2.16. Распределение газа по высоте hопределяется барометрической формулой: n(h) = n₀ехр(–mgh/kT), где n₀ – концентрация молекул в вершине воронки (при h = 0). Величины N и n₀ связаны соотношением:

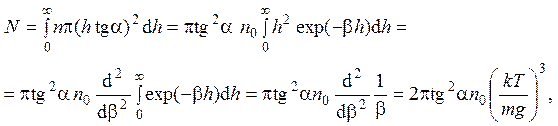где b = mg/kT.

Отсюда

n₀ = N/(2ptg²a)∙(mg/kT)³,    p₀ = n₀kT = N(mg)³/(kT)²/(2ptg²a).

Средняя потенциальная энергия молекулы

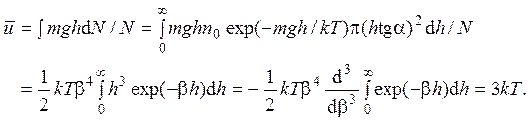
2.17. Полная энергия атома равна сумме кинетической и потенциальной энергий: e = mv²/2 + u(r). Кинетическая энергия определяется скоростью теплового движения атома, потенциальная зависит только от его положения. Поэтому статистическая сумма распадается на два множителя: Z = Z₁Z₂, где Z₁ соответствует распределению Максвелла, а Z₂ – распределению Больцмана. Таким образом, средняя энергия теплового движения атома равна ЗkТ/2. Чтобы найти среднее значение потенциальной энергии, надо вычислить статистическую сумму

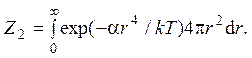
Здесь в качестве элемента объема рассматривается сферический слой радиуса r и толщины dr. Интеграл в элементарных функциях не вычисляется, но зависимость его от температуры может быть найдена. Для этого следует сделать замену переменных t = (α/kT)^1/4r. Тогда

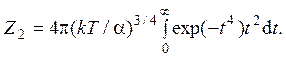
Интеграл в атом выражении для Z₂ является константой. Поэтому

ln Z₂ = const + ¾ lnT.

Средняя потенциальная анергия атома равна

Среднее значение энергии атома