Решебник по физике. Части 1-3 "Термодинамика", "Статистическая физика" и "Физическая кинетика", страница 12

Вода имеет очень малую сжимаемость. Поэтому изменением объема воды можно пренебречь. Поскольку энтропия – функция состояния, ее изменение не зависит от процесса. Для вычисления изменения энтропии воды реальный процесс выравнивания температуры заменяется изохорическим процессом. Тогда

S₂ – S₁ =  = = 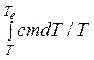cm×ln (T_e / T),

где m – масса воды, c – ее удельная теплоемкость.

От термостата к воде подводится количество теплоты

Q = cm(T_e  – T).

После подстановки выражений для S₂ – S₁ и Q (T_e = const) приведенное выше неравенство сводится к

ln (T_e / T) ≥ 1 – T / T_e ®   x = T / T_e   и  –ln x ≥ 1 – x,  или  ln x ≤ x – 1.

Если на плоскости x, y построить логарифмическую кривую y = ln x и провести прямую линию y = x – 1, то из графика на рисунке видно, что кривая лежит ниже прямой и лишь в точке (1, 0) они касаются.

Итак, в приведенном выше неравенстве знак «равно» имеет место только при T = T_e. Во всех остальных случаях (ниже температура воды или выше) выполняется строгое неравенство. Процесс теплообмена является неравновесным.

1.14. Свободная энергия F задана в естественных (канонических) переменных T и V. Следовательно, выражения для F достаточно для определения любой термодинамической характеристики системы. Из основного термодинамического тождества

TdS = dU + PdV

можно вывести выражение для приращения dF через приращения ее естественных переменных dV и dT. Замена переменных в основном термодинамическом тождестве осуществляется с помощью преобразования Лежандра:

TdS =dTS – SdT.

Отсюда

dTS – SdT= dU + pdV Þ d(U – TS ) = – SdT – pdV º dF

В первую очередь рассмотрим частные производные свободной энергии по ее естественным переменным. В частности, давление является ее частной производной

p = – (¶F/¶V)_T.

Вычисление его дает термическое уравнение состояния

p = RT/V.

Энтропия является частной производной свободной энергии по другой переменной

S = – (¶F/¶T)_V.

Ее вычисление дает

S = – a +b + b∙lnT + R∙lnV.

Исходя из определения свободной энергии, находится внутренняя энергия

U = F + TS = bT + c.

Далее вычисляется теплоемкость при постоянном объеме

C_V  = T(¶S/¶T)_V = b.

Проделанные вычисления подтверждают, что данная свободная энергия определяет термодинамику идеального газа. Можно убедиться, что и теплоемкость при постоянном давлении соответствует соотношению Майера

C_p = b + R.

1.15. Доказательство проводится для общего случая сред, характеризуемых объемом и давлением.

Наклон адиабат и изотерм определяется соответственно производными (¶р/¶V)_S и (¶р/¶V)_т. Следовательно, для решения задачи необходимо рассмотреть производную (¶р/¶V)_S и перейти от независимых переменных S, V к переменным т, V. Наиболее быстро результат может быть получен, если перейти от частных производные к якобианам и учесть, что теплоемкость с = Т(¶S/¶т). Итак,

(¶р/¶V)_S = ¶(S, р)/¶(S, V) = ¶(S, р)/¶(T, р) × ¶(T, р)/¶(T, V) ×  ¶(T, V)/¶(S, V) =

= (¶S/¶T)_р×(¶р/¶V)_T /(¶S/¶T)_V = C_p/C_V ×(¶р/¶V)_T,

отсюда следует, что

(¶р/¶V)_S £ (¶р/¶V)_т < 0.

1.16. По определению теплоемкости и с учетом второго начала термодинамики

C_V = (¶Q/¶T)_V = T(¶S/¶T)_V.

Поэтому, используя тот факт, что результат дифференцирования не зависит от последовательности дифференцирования, получаем:

(¶C_V/¶V)_T = T(¶²S/¶V¶T) = T¶(¶S/¶V)_T/¶T = T(¶²p/¶T ²)_V.

Здесь использовано, что (¶S/¶V)_T  = (¶p/¶T)_V. Оно получается с помощью калибровочного соотношения ¶(T, S)/¶(p, V) = 1, а именно:

(¶S/¶V)_T = ¶(T, S)/¶(T, V) = ¶(p, V)/¶(T, V) = (¶p/¶T)_V.